This morning it occurred to me that the problems we’re having with our equation \begin{align}S^2 Z^2 S^2 – S C S = \lambda (Z^{-1} – I)\label{main}\tag{1}\end{align} are due to the regularizer we use, $\|Z – I\|_F^2$. This regularizer makes the default behavior of the feedforward connections passing the input directly to the output. But it’s also where the $Z^{-1}$ comes from in $\Eqn{main}$, making the solution hard to understand.
If instead we change our regularizer to $\|Z^T Z – I\|_F^2$, then not only are solutions easier to understand, but we get a closed-form answer. In this case, the objective becomes $$ L(Z) = {1 \over 2} \|Y^T Y – X^T Z^T Z X \|_F^2 + {\lambda \over 2} \|Z^T Z – I\|_F^2.$$ This function only depends on $Z$ through $Z^TZ$, so letting $W = Z^T Z$, we instead optimize $$ L(W) = {1 \over 2} \|Y^T Y – X^T W X \|_F^2 + {\lambda \over 2} \|W – I\|_F^2.$$ Setting the gradient to zero, we get that $\wt{W}_{UU}$ (which I will just call $W$ below for brevity), satisfies $$ S^2 W S^2 – S C S = \lambda(I – W).$$ We can then explicitly solve for $W$ element-wise as $$ W_{ij} = {S_i S_j C_{ij} + \lambda \delta_{ij} \over S_i^2 S_j^2 + \lambda}.$$
Note that at this point we haven’t constrained $W$ at all. This can cause problems, as described below.
Problems
The closed-form solution above is great, but it comes with a few problems.
First, the solution is for $W = Z^T Z$. Therefore $Z$ is not completely specified. The same issue occurs in the decorrelation literature, where further constraints on $Z$ are used to yield unique solutions.
One such is the ZCA solution which constrains $Z = Z^T$. In that case, $W = Z^2$ so we can try simply taking $Z = \sqrt{W}.$ This would be fine except that for my data, $W$, while symmetric, has negative eigenvalues. The square root will produce connectivity with complex values, which seem hard to interpret, at the very least.
The root of this problem is that minimizing $L(W)$, without any additional constraints on $W$, won’t necessarily produce an answer that’s positive semi-definite. In fact, we were lucky that the answer was even symmetric when there was no explicit requirement that this be the case.
Another possibility is the PCA solution which requires that $ZZ^T$ equal some diagonal matrix $D$. In that case, we get $Z (Z^T Z) = Z W = D Z$ or equivalently $W Z^T = D Z^T$. This means that the rows of $Z$ are the eigenvectors of $W$, which, naively, seems very tough to compute and neurally implement.
An additional problem is the regularisation itself. A neural implementation of e.g. the ZCA case constrains $Z^2$ to be near $I$. Squaring mixes information about different synapses and implies that updating one synapse requires knowledge about many others – i.e. is non-local.
One possibility might be that the solutions of found with the original regularization are similar to those found with the new regularization, with the appropriate additional constraints on $Z$. But at least for ZCA, this does not seem to be the case:
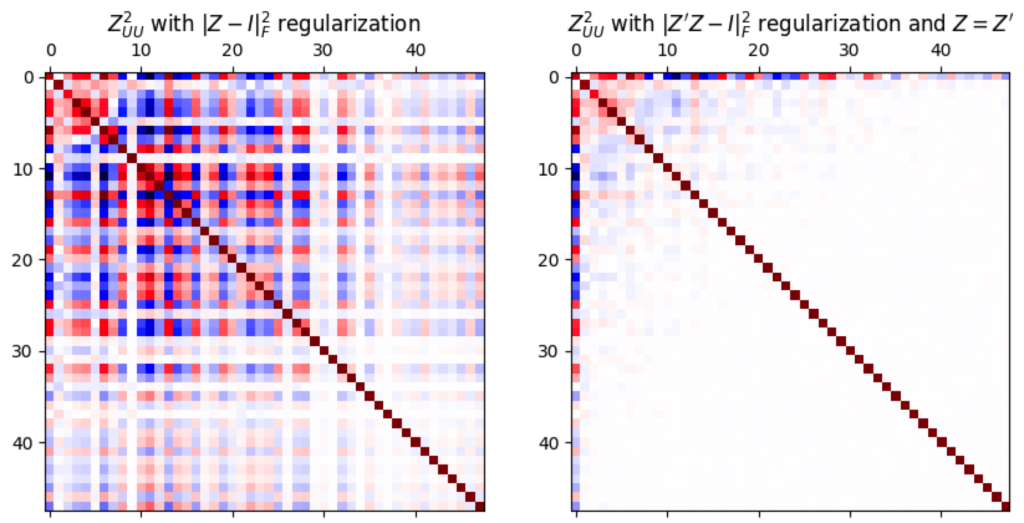
So I’ll keep this possibility in mind, but continue with my original regularization.
$$\begin{flalign*} && \phantom{a} & \hfill \square \end{flalign*}$$
Leave a Reply