These are my rapidly scribbled notes on Codol et al.’s “Brain-like neural dynamics for behavioral control develop through reinforcement learning” (and likely contain errors).
What learning algorithm does the baby’s brain use to learn motor tasks? We have at least two candidates: supervised learning (SL), which measures and minimizes discrepancies between desired and actual states moment-to-moment, and reinforcement learning (RL), which optimizes a value function determined by whether the desired final state was achieved. SL can be efficient but requires an accurate model of how actions affect outputs, while RL tends to be less efficient but only requires knowledge of reward.
The authors wanted to see which of these forms of learning were closer to what the brain does during a motor task. They trained a monkey to perform a reaching task while they recorded activity in motor cortex. They also trained two RNNs to control a model robot arm for the same task. One RNNs was trained using RL, the other using SL. The RNN architectures were identical, and the teaching signal used for both was the same,
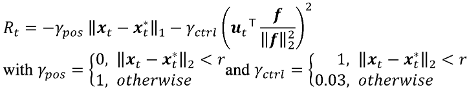
where $\xx_t$ is the current arm position, $\xx_t^*$ is the target position, and $\uu_t$ is the action vector, and $\mathbf f$ is the maximum contraction vector. So the first term penalizes errors in position, and the second term penalizes rapid actions. The SL network optimized this signal directly, while the RL network used it as a reward signal to train a value network and selected actions based on optimizing value.
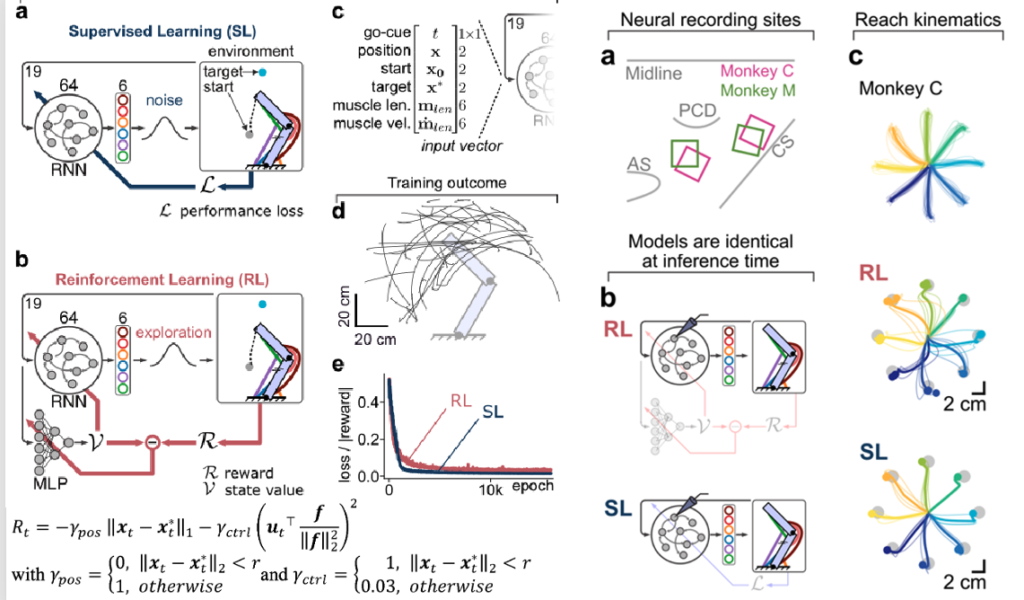
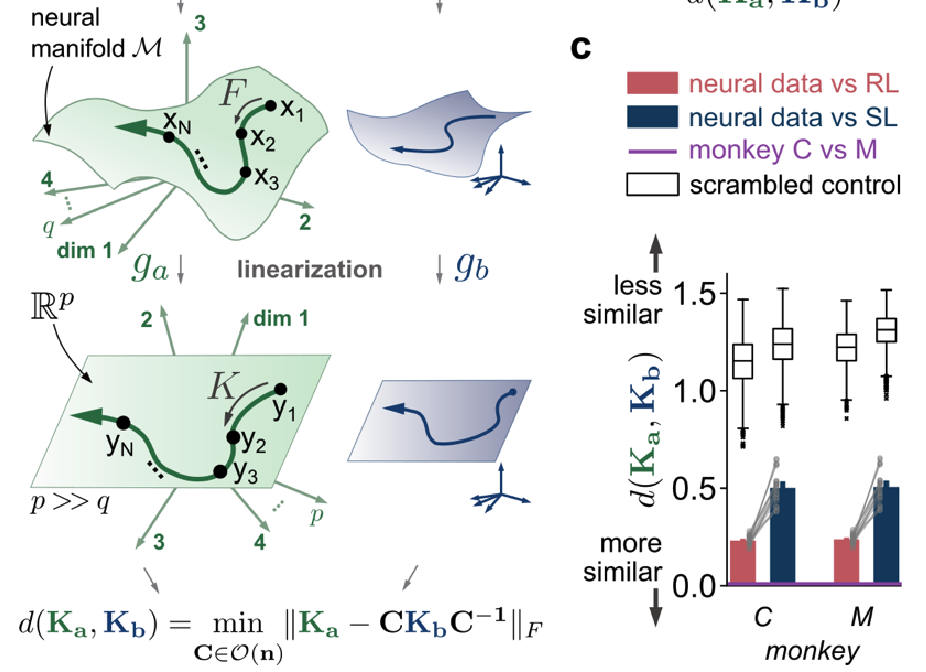
They compared neural geometry and dynamics to those of the two RNNs using PCA, CCA, DSA. The result of all of this was that the RNN trained using RL had more brain-like representations than the other. Here’s an example result using DSA:
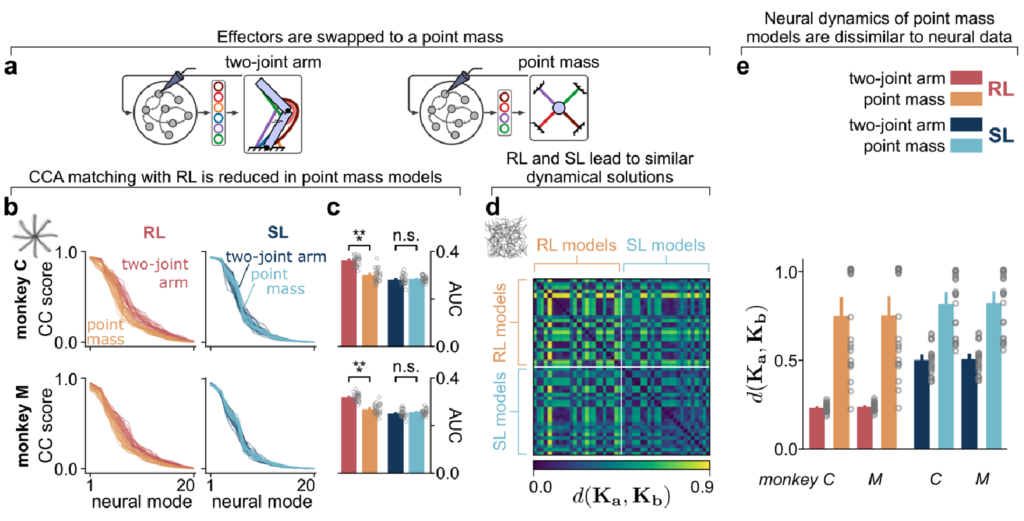
Next, they looked at the effect of the arm complexity. The arm they originally used was realistic and over-actuated. When they replaced it with a simpler arm, they found that both RNNs came up with the same solution:
Finally, they looked at the effect of perturbing the sensory-motor connection after learning, by shifting the cursor position of the arm by 30 degrees relative to the motion of the arm controlling it. They compared the change in representations after adaptation in monkeys and in the RNNs. For the RNNs, they considered all four combinations of pre-perturbation learning rule and post-perturbation learning rule. They found that using RL pre-perturbation was enough to get a good match to the adaptation regardless of the post-perturbation rule, producing a rotation in state. However, using SL pre-perturbation produced very different results. If SL was used post-perturbation as well, then the representation was translated, while if RL was used, the representation was scrambled:
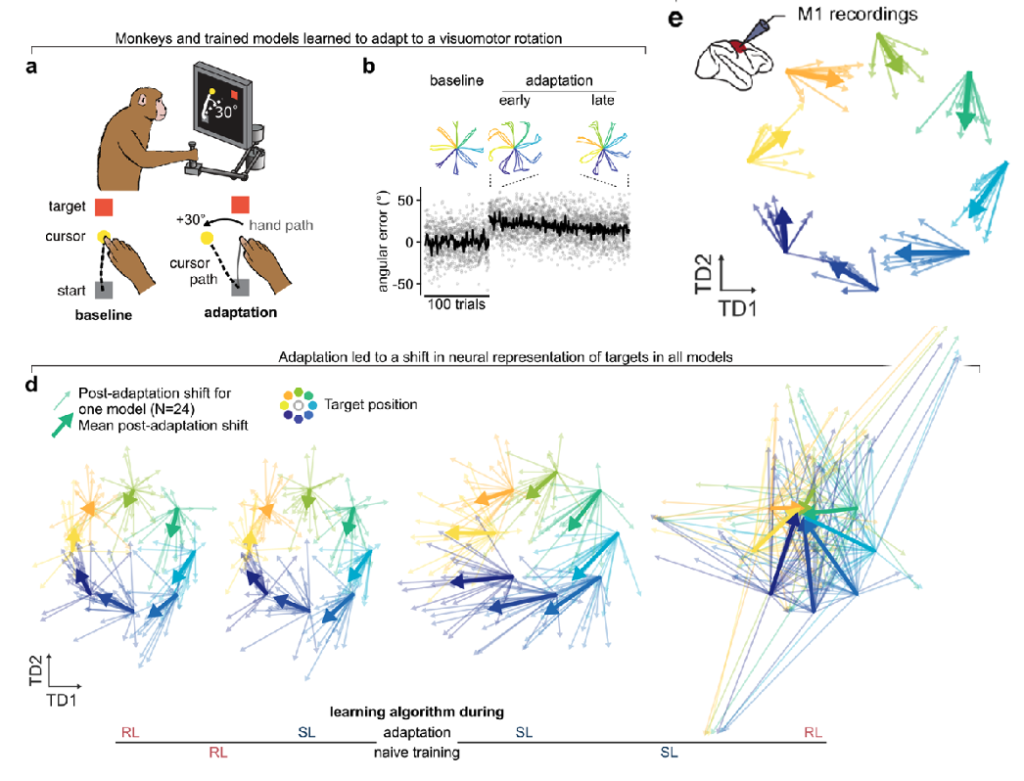
Their interpretation of this was that RL provides a good scaffold for adaptation for both methods, but that SL does not, only sufficing for SL, and forcing RL to learn an entirely new representation.
Remarks
The most interesting question for me is: what is it about RL that provides a more robust representation? Does the value function somehow smooth out the reward over state space? And how/why does it do that? Their arm is overactuated – when they used a simple arm, for which (presumably) only one solution was possible for the task, the two learning methods found it. But when there’s choice in solutions, RL seems to find a more robust one. Why is that? Why does it not find a more brittle solution still? It would have been very interesting if they tried an over-actuated version of their “simple” arm. Is it the complexity of the arm, or the overactuation? And there are intriguing parallels to how over-parametrized networks can learn effectively (although there the learning is by gradient descent). Is RL producing some kind of useful regularization of the gradient? Can we reproduce this in a simpler setting? So many interesting questions!
$$\blacksquare$$
Leave a Reply