In this post I expand on the details of section 3.1.2 in Pattern Recognition and Machine Learning.
We found that maximum likelihood estimation requires minimizing $$E(\mathbf w) = {1 \over 2} \sum_{n=1}^N (t_n – \ww^T \bphi(\xx_n))^2.$$ Here the vector $\bphi(\xx_n)$ contains each of our features evaluated on the single input datapoint $\xx_n$, $$\bphi(\xx_n) = [\phi_0(\xx_n), \phi_1(\xx_n), \dots \phi_{M-1}(\xx_n)]^T.$$ We’re interested in getting a deeper understanding of this minimization.
The way the error function is expressed above emphasizes the contribution of each datapoint. Another way to interpret that equation above involves changing our perspective from single datapoints to viewing the dataset as a whole. We do this by first packing all of the target values into a single $N$-dimensional vector $\tt$:
$$ \tt = [t_1, \dots, t_N]^T.$$ From this perspective, our entire set of $N$ target values is a single point in $N$-dimensional space.
Similarly, we pack our predictions for each observation into a single $N$-dimensional vector $\yy$: $$ \yy = [y_1, \dots, y_N]^T, \quad \text{where}\quad y_n = \ww^T \bphi(\xx_n).$$
We can now see that that error function above is simply twice the squared length of the difference between the target vector and our predictions, since
\begin{align} 2 E(\ww) &= \sum_{n=1}^N (t_n – \ww^T \bphi(\xx_n))^2\\ &=\sum_{n=1}^N (t_n – y_n)^2\\ &= \|\tt – \yy\|_2^2 .\end{align} So, minimizing the error function is the same as minimizing the distance between these two vectors.
To actually find a solution, we have to consider the range of values that our predictions $\yy$ can take, since any solution we find must live in that range. To do so, let’s expand $\yy$,
$$\yy = \begin{bmatrix} y_1 \\ \vdots \\ y_N \end{bmatrix} = \begin{bmatrix} \ww^T \bphi(\xx_1) \\ \vdots \\ \ww^T \bphi(\xx_N) \end{bmatrix} = \begin{bmatrix} \bphi(\xx_1) ^T \ww \\ \vdots \\ \bphi(\xx_N)^T \ww \end{bmatrix} = \begin{bmatrix} \bphi(\xx_1) ^T \\ \vdots \\ \bphi(\xx_N)^T \end{bmatrix} \ww = \bPhi \ww. $$ This tells us that $\yy$ is a linear combination of the columns of $\bPhi$ using weights $\ww$.
To see what the columns of $\bPhi$ actually are, let’s write it out explicitly,
$$ \bPhi = \begin{bmatrix} \bphi(\xx_1) ^T \\ \vdots \\ \bphi(\xx_N)^T \end{bmatrix} = \begin{bmatrix} \phi_0 (\xx_1), & \dots , &\phi_{M-1} (\xx_1) \\\phi_0 (\xx_2),& \dots, &\phi_{M-1} (\xx_2) \\
\vdots\\
\phi_0 (\xx_N),& \dots, &\phi_{M-1} (\xx_N) \end{bmatrix} = [\bvphi_0 (\xx), \dots \bvphi_{M-1}(\xx)].$$ Here $\bvphi_j(\xx)$ is the vector of feature $j$ evaluated on all the datapoints,
$$\bvphi_j(\xx) = [\phi_j(\xx_1), \dots, \phi_j(\xx_N)]^T.$$
Notice the two perspectives: we can either view $\bPhi$ as a stack of $N$ rows, where each row $\bphi(\xx_n)$ is every feature evaluated on one data point, or as a stack of $M$ columns, where each column $\bvphi_j(\xx)$ is one feature evaluated on every data points. It’s the latter view which is particularly insightful because it allows us to express our predictions $\yy$ for the entire dataset, as a linear combination of the different features evaluated on the entire dataset,
$$\yy = \bPhi \ww = \sum_{j=0}^{M-1} \bvphi_j(\xx) w_j.$$
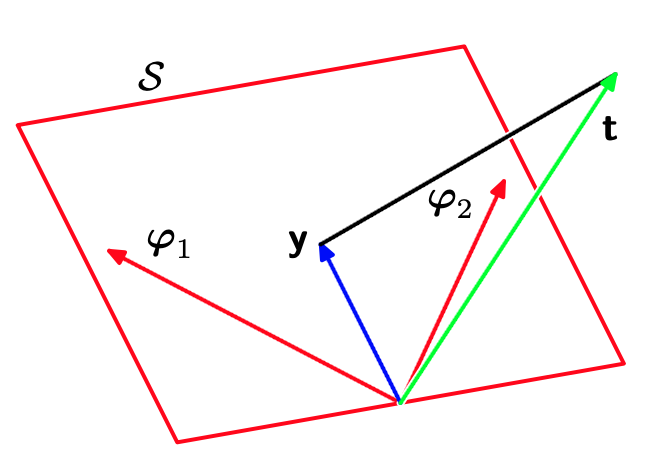
Returning to our minimization problem, we can see now that since we are free to set the weights $\ww$ to any value we like, the range of predictions $\yy$ available to us when performing the minimization are any linear combination of the feature $\bvphi_j$. The set of all such points forms a plane through the origin called the span of the features. The figure above shows the span $\mathcal S$ for two features $\bvphi_1$ and $\bvphi_2$.
The geometric solution to our problem is then clear: we want to find the point in the span of the features that is as close as possible to the target vector $\tt$. We can also now see that a “good” set of features is one whose span comes close to the target vector.
Ideally, the span would contain the target vector, meaning we could reduce the error to zero. When we have fewer features than observations, which is the case we’re considering here, this won’t be possible in general. Instead, we’ll settle for the point in the span that’s closest to the target vector. We will now find this point in three different ways.
Approach 1: Gradient descent
This is perhaps the simplest method and does not require any geometric insight. We simply compute the gradient of the error function with respect to $\ww$, set it to zero, and report the answer. Because our error function is bowl-shaped (more on this later), it has only one location where the gradient is zero, so we don’t have to worry about multiple solutions, local minima, etc.
The gradient of our error function with respect to $\ww^T$ is
$$ \nabla_{\ww^T} E =- \sum_n (t_n – \ww^T \bphi(\xx_n)) \bphi(\xx_n)^T.$$ It’s (subjectively) nicer to work with $\ww$ than $\ww^T$, so let’s transpose both sides and get the derivative with respect to $\ww$ as $$ \nabla_{\ww} E =- \sum_n (t_n – \ww^T \bphi(\xx_n)) \bphi(\xx_n).$$
Setting this to zero we get $$ \sum_n t_n \bphi(\xx_n) = \left(\sum_n \bphi(\xx_n) \bphi(\xx_n)^T\right) \ww.$$
The left-hand side is a linear combination of our transformed inputs, so we can write it compactly as
$$ \sum_n t_n \bphi(\xx_n) = [\bphi(\xx_1) \dots \bphi(\xx_N)] \begin{bmatrix}t_1 \\\vdots\\t_N\end{bmatrix} = \bPhi^T \tt.$$
As for the right-hand side, we recall the very useful observation that to multiply two matrices, we can sum up the outer products of one column from the first and a corresponding row from the second. That is, if $$\AA = [\aa_1, \dots, \aa_N], \text{ and } \BB = \begin{bmatrix}\bb_1^T \\\vdots\\\bb_N^T\end{bmatrix},$$ then $$ \AA \BB = \sum_n \aa_n \bb_n^T.$$
Recognizing a sum like that in the equation for $\ww$ above, we get $$\left(\sum_n \bphi(\xx_n) \bphi(\xx_n)^T\right) \ww = \bPhi^T \bPhi \ww.$$ Putting the two pieces together, we get $$ \bPhi^T \tt = \bPhi^T \bPhi \ww.$$
Since $\Phi$ has more rows than columns, $\bPhi^T \bPhi$ will in general be invertible, so we apply its inverse on the left to both sides to get
$$ (\bPhi^T \bPhi)^{-1}\bPhi^T \tt = \hat \ww,$$ where the hat indicates our solution for the weights. To get the our actual predictions, $$ \hat \yy = \bPhi \hat \ww = \bPhi (\bPhi^T \bPhi)^{-1}\bPhi^T \tt.$$
This equation can seem a bit mysterious. We’ll try to clear up some of the mystery a little later. For now, let’s at least do a sanity check. Recall that the reason we can’t minimize the error to zero is because our target vector $\tt$ is $N$-dimensional, and our span is only $D$-dimensional. So the target will live off of the span in general. However, If we had exactly as many observations as features, then the dimensionality of our targets would equal the span, meaning that our predictions should match the targets exactly. Let’s check that our equation above gives the same answer in this case.
When we have as many observations as features, $\bPhi$ will be a square matrix, and will (usually) be invertible, and therefore $\bPhi^T \bPhi$ will be as invertible. Then,
\begin{align}
\hat \yy &= \bPhi (\bPhi^T \bPhi)^{-1} \bPhi^T \tt\\
&= \bPhi(\bPhi^{-1} \bPhi^{-T}) \bPhi^T \tt\\
&= \bPhi \bPhi^{-1} \bPhi^{-T} \bPhi^T \tt\\
&= \tt, \end{align} as we hoped. So, at least in this special case, our formula above gives the right answer.
Approach 2: The Orthogonality Principle
The first approach was very mechanical and not very geometric. In our second approach we will use geometry to avoid calculus! In particular, we’ll use the simple observation that the point in the span closest to the target vector is “directly below” it. In other words, the vector we’re trying to minimize, $\tt – \yy$, which points from our solution, which lives in the span, to the target vector, will be perpendicular (orthogonal) to the span. So all we have to do is find a $\hat \yy$ such that $\tt – \hat \yy$ is orthogonal to the span.
But how do we do that? Since the span is generated by all linear combinations of our feature vectors $\bvphi_j$, it suffices to check that $\tt – \hat \yy$ is orthogonal to each one of these feature vectors, i.e. $$ \bvphi_j^T (\tt – \hat \yy) = 0, \quad \text{for all } j.$$ If we can find such a $\hat \yy$, then we’re guaranteed that $\tt – \hat \yy$ is orthogonal to the span, because for any point in the span $\pp = \sum_j p_j \bvphi_j,$ $$\pp^T (\tt – \hat\yy) = \sum_j p_j (\bvphi_j^T (\tt – \hat \yy)) = 0.$$
We can write our orthogonality condition above as $$ \bvphi_j^T \tt = \bvphi_j^T \hat \yy, \quad \text{for all } j.$$ We can write this as one matrix equation, with one row for each feature,
$$ \begin{bmatrix} \bvphi_1^T \tt \\ \vdots \\ \bvphi_{M-1}^T \tt \end{bmatrix} = \begin{bmatrix} \bvphi_1^T \hat \yy \\ \vdots \\ \bvphi_{M-1}^T \hat \yy \end{bmatrix}.$$
Since $\tt$ on the left-hand side is the same in each row, we can bring it out of the matrix, and similarily for $\hat \yy$ on the right hand side, so $$ \begin{bmatrix} \bvphi_1^T \\ \vdots \\ \bvphi_{M-1}^T \end{bmatrix} \tt = \begin{bmatrix} \bvphi_1^T \\ \vdots \\ \bvphi_{M-1}^T \end{bmatrix} \hat \yy.$$
Our design matrix $\bPhi$ had the features as its columns, whereas the matrix above has the features as its rows, and we recognize the transpose of the design matrix. We can then write our conditions as
$$ \bPhi^T \tt = \bPhi^T \hat \yy.$$
To get the solution in terms of $\hat \ww$, we recall that $\hat \yy = \bPhi \hat \ww,$ so$$ \bPhi^T \tt = \bPhi^T \bPhi \hat \ww.$$ Solving for $\hat \ww$ as before, we get
$$ (\bPhi^T \bPhi)^{-1} \bPhi^T \tt = \hat \ww,$$ the same solution as before (whew!) but without any calculus!
Approach 3: Direct projection using SVD
We’ve seen above that the solution we’re after is the orthogonal projection of the target vector into the span of the features. If we had an orthonormal coordinate system for this span, we could compute this projection easily by simply projecting the target vector into each of these coordinates.
To get such a coordinate system, we apply the singular value decomposition to our design matrix. We’ll find it useful to express $\bPhi$ from the two perspectives: $$ \bPhi =[\bvphi_0(\xx), \bvphi_1(\xx), \dots, \bvphi_{M-1}(\xx)] = \begin{bmatrix} \bphi(\xx_1)^T \\ \bphi(\xx_2)^T\\\vdots\\\bphi(\xx_N)^T\end{bmatrix} = \UU \SS \VV^T.$$ Here $\UU$ is an $N \times (M-1)$ matrix whose columns form an orthonormal basis for the space spanned by our features. Our solution should then be
$$ \hat \yy = \UU \UU^T \tt.$$ To see why this works, multiply the matrices like we did above to get $$\UU \UU^T = \sum_i \uu_i \uu_i^T,$$ where $\uu_i$ is the $i$’th column of $\UU$. When we apply $\UU \UU^T$ to $\tt$, we get
$$ \UU \UU^T \tt = \sum_i (\uu_i \uu_i^T) \tt = \sum_i \uu_i (\uu_i^T \tt) = \sum_i \uu_i t_i.$$ So $\UU \UU^T \tt$ produces a linear combination of the columns of $\UU$, weighting each combination by the the projection of $\tt$ onto the corresponding column.
Does the solution we found by direct projection match our previous solutions? Recall that we had $$ \hat \yy = \bPhi (\bPhi^T \bPhi)^{-1} \bPhi^T \tt.$$ Using SVD, we can write this as \begin{align} \hat \yy &= (\UU \SS \VV^T)(\VV \SS^2 \VV^T)^{-1} (\VV \SS \UU^T) \tt\\
&=(\UU \SS \VV^T)(\VV \SS^{-2} \VV^T) (\VV \SS \UU^T) \tt\\&=\UU \SS (\VV^T \VV) \SS^{-2}( \VV^T \VV) \SS \UU^T\tt\\&=\UU \SS \SS^{-2} \SS \UU^T\tt\\&=\UU \UU^T \tt,\end{align} the direct projection that we proposed above.
What is $\bPhi^T \bPhi$?
Since $\bPhi = [\bvphi_0(\xx), \dots \bvphi_{M-1}(\xx)]$, $\bPhi^T \bPhi$ is a matrix whose elements are the dot products of our features with each other: $$[\bPhi^T \bPhi]_{ij} = \bvphi_i(\xx)^T \bvphi_j(\xx).$$ High values indicate that a pair of features are quite similar. We care about this because, intuitively, we compute our estimate by first projecting the targets into the space of our features (forming $\bPhi^T \tt$). This is also sometimes called the analysis step, because we’re decomposing, or analyzing, our input into its projections onto our features.
We then construct our estimate as a linear combination of those features. This is the synthesis step, because we’re synthesizing our estimate!
If we simply performed the synthesis by weighting our features by their projections on the input, $$\hat \yy = \bPhi \bPhi^T \tt,$$ we would end up “double-counting” features with high overlap.
To see this, let’s imagine that our design matrix is really simple, the identity, so $\bPhi = \II$. Our estimate of any input $\tt$ would be $$ \hat \yy = \II \, \II^T \tt = \tt,$$ so (unsurprisingly) our estimate matches the input perfectly.
Now let’s try the same procedure but with a design matrix where we can adjust the amount of overlap between the features. We’ll do this by adding $\epsilon$ to every element of our design matrix, and we’ll call the result $\II_\epsilon$,$$ \II_\epsilon = \II + \epsilon \mathbf{11^T} = \begin{bmatrix}1 + \epsilon & \epsilon, &\dots, &\epsilon\\
\epsilon, &1 + \epsilon, &\dots, &\epsilon\\
\vdots\\
\epsilon, &\epsilon, &\dots, &1 + \epsilon\end{bmatrix}.$$
The overlaps for this design matrix are $$\II_\epsilon^T \II_\epsilon = (\II + \epsilon \mathbf{1 1}^T)^T (\II + \epsilon \mathbf{1 1}^T) = \II + (2 \epsilon + n \epsilon^2) \mathbf{11}^T = \II + \delta \mathbf{11}^T,$$ where I’ve defined $\delta = 2 \epsilon + n \epsilon^2$ to avoid having to write all that out. This matrix has the same form as our design matrix $\II_\epsilon$ above, just with $\epsilon$ replaced by $\delta$. We can see that $\delta$ allows us to adjust the degree of overlap, as desired.
To compute our estimate, we need $\II_\epsilon \II_\epsilon^T$, but this is the same as $\II_\epsilon^T \II_\epsilon$ for our design matrix since it’s symmetric. When we apply our simple estimation procedure from before, we get $$ \hat \yy = \II_\epsilon \II_\epsilon^T \tt = (\II + \delta \mathbf{11}^T)\tt = \tt + \delta \mathbf 1 \mathbf 1^T \tt = \tt + \left(\delta \sum_i t_i\right) \mathbf 1 $$
So, in addition to $\tt$, our estimate now includes an extra term that’s related to the sum of the elements of $\tt$. This addition takes us farther from the optimal estimate of $\hat \yy = \tt$. It’s clearly contributed by the overlaps we introduced and reflects the fact that we didn’t account for these overlaps when synthesizing our estimate.
That’s where $\bPhi^T \bPhi$, or in our case, $\II_\epsilon^T \II_\epsilon$ comes in. We use its inverse, $(\II_\epsilon^T \II_\epsilon)^{-1}$, to cancel out the effect of the overlaps. Let’s first compute the inverse. Applying the very useful Sherman-Morrison formula, $$(\II_\epsilon^T \II_\epsilon)^{-1} = (\II + \delta \mathbf{11}^T)^{-1} = \II – {\delta \over 1 + \delta n} \mathbf{11}^T.$$ This matrix is again of the same form as $\II_\epsilon$ – the identity, plus a single value added to every element – but now this value is negative, so acts in the opposite direction to the overlaps to cancel them out.
When we then sandwich this adjustment between our analysis and synthesis steps, we get the result we were after, \begin{align} \hat \yy &= \II_\epsilon (\II_\epsilon^T \II_\epsilon)^{-1} \II_\epsilon^T \tt\\
&= \II_\epsilon \left[\II – {\delta \over 1 + \delta n} \mathbf{11}^T\right]
\II_\epsilon^T \tt\\ &= \left(\II_\epsilon \II_\epsilon^T – {\delta \over 1 + \delta n} \II_\epsilon \mathbf{1 1}^T \II_\epsilon^T \right)\tt\\&= \left(\II + \delta \mathbf{1 1}^T – \delta{(1 + n \epsilon)^2 \over 1 + \delta n} \mathbf{1 1}^T \right)\tt\\&= \left(\II + \delta \mathbf{1 1}^T – \delta\mathbf{1 1}^T\right)\tt\\&=\II \tt \\&=\tt.\end{align} So, once we account for the overlap, our estimation procedure returns the target vector, as it should.
Above, we picked a particularly simple design matrix example to help us understand what’s going on. But the same basic idea holds in the general case, which we can see using SVD. To do that, we can go back to our direct projection example and look carefully at how we computed our estimate. We had
$$ \hat \yy = \underbrace{(\UU \SS \VV^T)}_{\bPhi: \text{synthesis}}\; \underbrace{(\VV \SS^{-2} \VV^T)}_{(\bPhi^T \bPhi)^{-1}: \text{adjustment}}\; \underbrace{(\VV \SS \UU^T)}_{\bPhi^T: \text{analysis}} \tt.$$
Notice what’s happening here: after projecting $\tt$ onto $\UU^T$, we expand the result by the singular values in $\SS$ and use the projections to form a linear combination of the columns of $\VV$. But then — and this is where $(\bPhi^T\bPhi)^{-1}$ comes in — we immediately go back to the projection coefficents using $\VV^T$, attenuate by the square of the singular values ($\SS^{-2}$), then form the linear combination of $\VV$ again. Why attenuate by the square of the singular values? Because we’re going to do one more round of expansion on the way out: we again go back to the projection coefficients using $\VV^T$, expand once more by $\SS$, and use the result to combine the columns of $\UU$ and form our output. So we can view the role of $(\bPhi^T \bPhi)^{-1}$ as undoing the (double) expansion that we apply to the input, changing it as little as we can. This makes sense, because we’re trying to make the output as similar as possible to the input, and any unnecessary expansions or contractions would take us away from the best solution.
Finally – there’s exactly one minimum
We’ve found one solution above, how can we be sure it’s the only one? Our geometric perspective convinces us that’s the case because given a point off of a plane, there is exactly one point on the plane closest to it. To see this analytically, we just go back to our equation for the gradient, $$\nabla_\ww E = -\bPhi^T (\tt – \bPhi \ww),$$ and differentiate with respect to $\ww$ one more time to get the curvature of our function$$ \nabla_\ww \nabla_\ww E = \bPhi^T \bPhi = \VV \SS^2 \VV^T.$$
We can then compute the curvature along the directions given by the columns $\vv_i$ of $\VV$ and get $$ \vv_i^T \VV \SS^2 \VV^T \vv_i = s_i^2.$$ What this says is that if we rotate our coordinate axes to be the columns of $\VV$, then we will find that our function has constant positive curvature ($s_i^2>0$) along each of the coordinate directions $\vv_i$. In other words, our function is a (multi-dimensional) parabola, and will have exactly one minimum…and which we can find in at least three different ways. 🙂
$$\blacksquare$$
Leave a Reply