Yesterday I went to discuss the problem with one of my colleagues. He had the interesting idea of modelling $S$, and especially $S^2$, as low rank, in particular as $S = s_1 e_1 e_1^T$. That is, shifting the focus on $S$ from $Z$. I tried this out today, and although it didn’t quite pan out, the discussion we had sent me on a useful trajectory that I will describe in this post.
As always in this series, the equation whose solutions we’re trying to understand is \begin{align}S^2 Z^2 S^2 – S C S = \lambda (Z^{-1} – I).\label{main}\tag{1}\end{align} I returned to approximating $Z$, and considered approximations for which $Z^2$ and $Z^{-1}$ are in the same ‘family’. For example, if $Z \approx I + uu^T$, then
\begin{align} Z^2 &= I + (2 + u^T u) uu^T, \\Z^{-1} &= I – {1 \over 1 + u^T u} uu^T.\end{align} Both of these are of the form $I + \beta uu^T$, so there might be some hope of equating coefficients of $uu^T$ on the left and right sides of $\Eqn{main}$. When I plugged in this form for $Z$, I was able to derive an interesting eigenvalue relationship that $u$ satisfies.
I found earlier in the week that $Z$ can be approximated as a low-rank update to a diagonal matrix, as shown on the far left below:
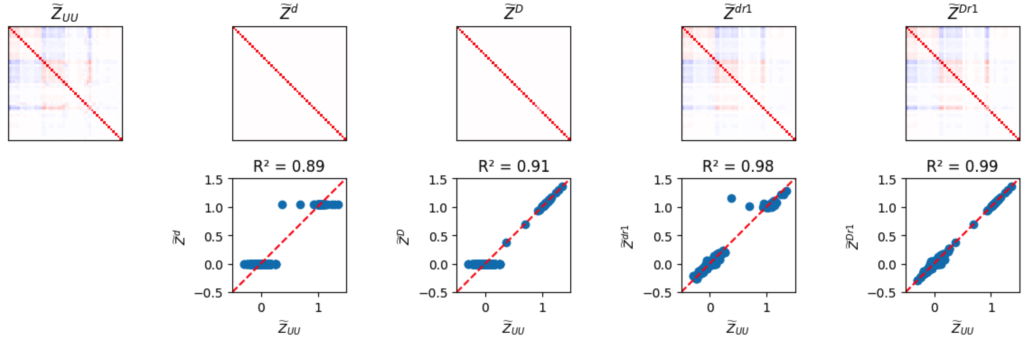
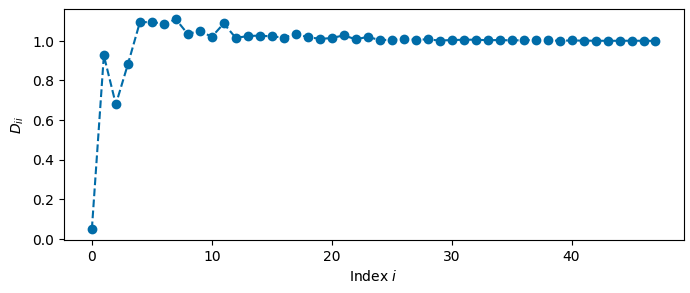
Unfortunately, the diagonal matrix is not quite the identity. In particular, its first value is very close to zero:
However, the success I had with deriving an eigenvalue equation for the $I + uu^T$ approximation motivated me to try to derive one here as well.
We first need $Z^2$ and $Z^{-1}$:
\begin{align} Z &\approx D + uu^T, \\
Z^2 &\approx D^2 +D uu^T + uu^T D + (u^T u) uu^T,\\
Z^{-1} &\approx D^{-1} – {D^{-1} uu^T D^{-1} \over 1 + u^T D u}.\end{align}
Plugging these into $\Eqn{main}$ gives
$$ {S^2 (D^2 + D uu^T + uu^T D + (u^T u) uu^T )S^2 – S C S \over \lambda} + I = D^{-1} – {D^{-1} u u^T D^{-1} \over 1 + u^T D^{-1} u}.$$
Multiplying both sides by $u$ gives
$$ {(\Lambda_1 + \Lambda_2 + \Lambda_3 + \Lambda_4) u – S C S u \over \lambda} = \left[\left(1 – {u^T D^{-1} u\over 1 + u^T D^{-1} u}\right) D^{-1} – I\right]u,$$ where I’ve defined the diagonal matrices \begin{align} \Lambda_1 &= S^2 D^2 S^2, & \Lambda_2 &= (u^T S^2 u)S^2 D,\\ \Lambda_3 &= (u^T D S^2 u) S^2, & \Lambda_4 &= (u^T u) (u^T S^2 u) S^2.\end{align}
Then, largely because of how small $D_{11}$ is, a few amazing things happen.
First, the matrix on righthand side becomes approximately $-I + 2e_1e_1^T$.
Second, the elements of $\Lambda_4$, especially the first few, are much larger than the rest, so we can approximate $$ \sum_{i=1}^4 \Lambda_i \approx \Lambda_4.$$ Although e.g. $\Lambda_1$ has $S^4$ in it, the presence of $D^2$ appears enough to squash its influence. $\Lambda_4$ is the only term that doesn’t have $D$ in it, and it dominates the others.
Third, $|\Lambda_4 / \lambda| \gg 1$ for almost all the elements, so we can ignore the righthand side.
So, after these three amazing effects, we end up with
$$ \Lambda_4 u = (u^T u) (u^T S^2 u) S^2 u \approx S C S u.$$ Left multiplying by $S^{-1}$ we get $$ (u^T u) (u^T S^2 u) S u \approx C S u.$$ In other words, $S u$ is an eigenvector of $C$ with eigenvalue $(u^T u) (u^T S^2 u).$
Not quite sure what this all means, but an interesting result.
$$\begin{flalign*} && \phantom{a} & \hfill \square \end{flalign*}$$
Leave a Reply