In the last post on this topic, we saw that when optimizing the objective
$$ {1 \over 2 n^2 } \|X^T Z^T Z X – C\|_F^2 + {\la \over 2 m^2}\|Z – I\|_F^2,$$ any solution $Z$ is symmetric and satisfies $${2 \over n^2} \left( XX^T Z^2 XX^T – X C X^T\right) + {\la \over m^2} I = {\la \over m^2} Z^{-1}.$$ In this post we’re going to conclude the analysis.
Since $Z$ is symmetric, we can decompose it into orthogonal components as $$ Z = Z_{UU} + Z_{QQ} = U \wt Z_{UU} U^T + Q \wt Z_{QQ} Q^T,$$ where $Q$ is an orthonormal completion of the matrix $U$ given below. We will see that the objective only relates to the $\wt Z_{UU}$ component, so any regularization $\la > 0$ will pull $\wt Z_{QQ}$ to the identity, $$ \la >0 \implies \wt Z_{QQ} = I \implies Z_{QQ} = QQ^T.$$ So for the rest of the post we will try to determine $Z_{UU}$.
Decomposing $X$ as $U S V^T$, we have after slightly rearranging
$$ {2 m^2 \over \la n^2} \left(U S^2 U^T Z^2 U S^2 U^T – U S V^T C V S U^T\right) + I = Z^{-1}.$$ Letting $\wt Z_{UU} = U^T Z U$ and $\wt C_{VV} = V^T C V$, we left-multiply by $U^T$ and right-multiply by $U$ to get
$$ {2 m^2 \over \la n^2} \left(S^2 \wt Z_{UU}^2 S^2 – S \wt C_{VV} S \right) + I = \wt Z_{UU}^{-1}.$$
Now in general $\wt{Z}_{UU}$ can be any symmetric square matrix, and this equation would be hard to solve. But in our case, the singular values of $X$ drop off very rapidly. Below I’ve plotted the singular vectors for a random subsample of the trials, along with the corresponding left and right singular vectors and the response mode.
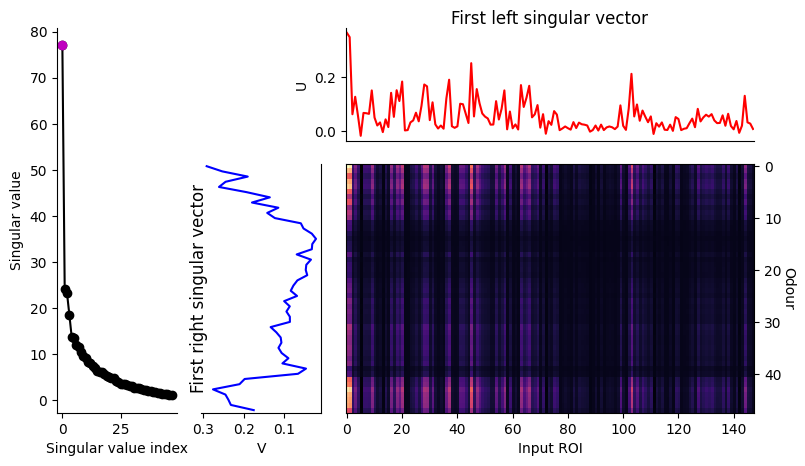
Therefore, left and right multiplying a matrix like $\wt {C}_{VV}$ with $S$, or $\wt{Z}_{UU}^2$ with $S^2$, will squash all but the first row and first column. Adding the identity to this will make the result approximately an arrowhead matrix,
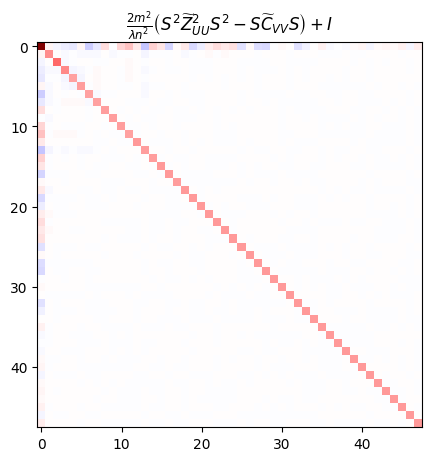
Inverting this matrix will give us $\wt Z_{UU}$. Let’s pack the terms being added to the identity into the variable $H$:
$$ H \triangleq {2 m^2 \over \la n^2} \left(S^2 \wt Z_{UU}^2 S^2 – S \wt C_{VV} S \right).$$ If we call the leftmost column of this matrix $h$, then the corresponding arrowhead matrix has inverse $$ (H + I)^{-1} = \wt Z_{UU} = I – e_1 e_1^T + {\tilde h \tilde h^T \over h_0},$$ where $$ \tilde h =[1, -h_2, -h_3, \dots], \quad h_0 = 1 + h_1 – \|\tilde h\|_2^2.$$
We can go further and assume that $h_1$ is much larger than the remaining terms in $h$, in which case we arrive at an identity + rank 1 approximation
$$ h_1 \gg h_2, h_3 \dots \implies I – e_1 e_1^T + {\tilde h \tilde h^T \over h_0} \approx I – e_1 e_1^T + {e_1 e_1^T \over 1 + h_1} = I – {h_1 e_1 e_1^T \over 1 + h_1}.$$ Here is how they compare against the true values of $(H + I)^{-1}$:
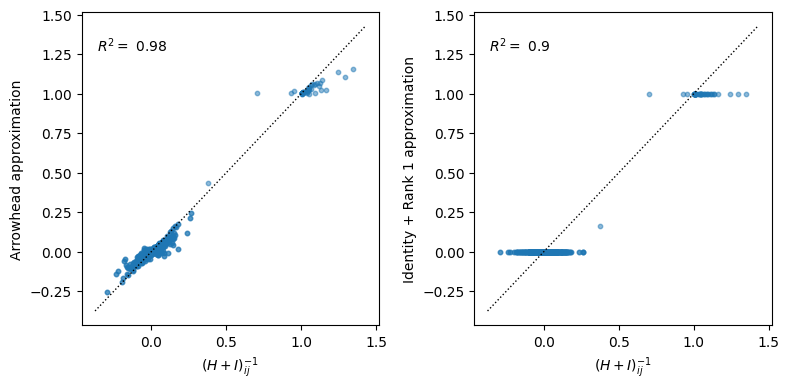
The arrowhead approximation is pretty good, and the identity+rank 1 approximation, although of course worse, isn’t too bad. We can then use these approximations instead of $\wt{Z}_{UU}$ to compute $Z_{UU}$, in which case,
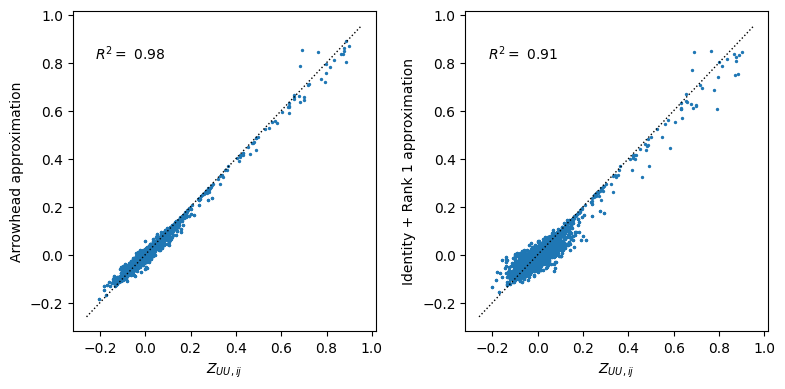
A very good match when using the arrowhead approximation, and not too bad when using the identity + rank 1, given its simplicity.
Solving for $h_1$
From our expression for $H$ we can read off $h_1$ as $$ h_1 = e_1^T H e_1 = {s_1^2 \over \lambda’}(s_1^2 e_1^T \wt Z^2_{UU} e_1 – v_1^T C v_1),$$ where we’ve defined $\la’ = \la n^2 / 2 m^2$ and $s_1$ is the largest singular value. If we use the identity + rank 1 approximation for $h_1$, \begin{align}\wt{Z}_{UU} &\approx I – {h_1 e_1 e_1^T \over 1 + h_1}\\ \wt{Z}_{UU}^2 &\approx I + \left({h_1^2 \over (1 + h_1)^2} – {2 h_1 \over 1 + h_1}\right)e_1 e_1^T\\&= I + {h_1^2 -2h_1 – 2h_1^2 \over (1 + h_1)^2} e_1 e_1^T\\&= I – {2h_1 + h_1^2 \over (1 + h_1)^2} e_1 e_1^T\end{align} the top-left corner element is
$$ e_1^T \wt{Z}^2_{UU} e_1 \approx 1 – {2h_1 + h_1^2 \over (1 + h_1)^2} = {1 \over (1+h_1)^2}.$$ Substituting this into the righthand side of the expression for $h_1$, we get
$$ h_1 = {s_1^2 \over \la’}\left({s_1^2 \over (1 + h_1)^2} – c \right), $$ where $c = v_1^T C v_1.$ We then arrive at the cubic equation $$ \la’ h_1 (1 + h_1)^2 + c s_1^2 (1 + h_1)^2 – s_1^4 = 0.$$ Adding and subtracting $\la'(1+h_1)^2$, and defining $x = 1 + h_1$, we get $$\la’ x^3 + (c s_1^2 – \la’) x^2 – s_1^4 = 0.$$
When I actually plug in some numbers for this, I find that $x$ comes out to being about 1.16, so $h_1 = x – 1 = 0.16$. But the true value is around 5! So this is a poor approximation.
I think part of the problem can be seen in our initial equation for $H$. The lefthand side is all order 1. The constant on the right hand side is $10^{-5}$, the $S^2$ can be nearly to $10^4$, and $\wt C_{VV}$ is $10^3$. So if we our approximation deviates by $\varepsilon$ from the true value $Z^*$, then $$ 10^0 = 10^{-5} (10^4 \; (Z^* \pm \varepsilon) \; 10^4 – 10^7) = \text{true value} \pm 10^3 \varepsilon.$$ So I need $\varepsilon < 10^{-3}$ to not perturb the result too much. But my approximations aren’t that accurate.
I’m going to need another way to estimate $h$.
Leave a Reply