The projection neurons of the olfactory bulb are the mitral cells and tufted cells. Most mitral cells don’t communicate with each other directly. Instead, they interact through the synapses that their lateral dendrites make onto granule cell abors. Activation of these synapses excites the target granule cells, which in turn inhibit the mitral cells that contact their arbors. The activity of the granule cells thus coordinates the interactions of mitral cells. An interesting question is then how many mitral cell lateral dendrites can cross a granule cell arbor.
Mitral cells only have a small number of lateral dendrites, but these are very long, with lengths of 1 mm or more. In comparison, granule cell arbors are relatively narrow, with radii on the order of 100 um.
To model the lateral dendrite crossings, we will assume that mitral cells are randomly distributed at a uniform density of $\rho$ on the mitral cell layer. Each mitral cell will have $n$ lateral dendrites of length $L$ extending outwards from the cell body. The directions of these lateral dendrites will be evenly distributed around the circle and with a random angular offset.
To compute the expected number of arbor crossings, we will take the perspective of arbor located at the origin $(0,0)$. We will first compute the expected number of crossings of lateral dendrites coming from a single mitral cell at location of $(-R,0)$. The maximum angle that a lateral dendrite from this mitral cell can take relative to the $x$-axis to still intersect the arbor is $$ \arcsin\left(r \over R\right) \triangleq {\phi \over 2}.$$

If a mitral cell had a single randomly oriented lateral dendrite, the odds of it pointing in the right direction would be $\phi/2 \pi$. To see this, consider the situation where instead of the granule cell being fixed and the lateral dendrites having a random orientation, the lateral dendrite is fixed on the x-axis, and the granule cell has a random rotation around the mitral cell. The lateral dendrite will intersect the granule cell arbor whenever the granule cell’s random rotation relative to the mitral cell is $\pm \phi/2$ radians, which will happen $\phi/2\pi$ of the time.
When we have $n$ lateral dendrites per mitral cell, then each lateral dendrite has a zone of $\pm \phi/2$ radians around it where it can cross the granule cell arbor. Therefore, the expected number of lateral dendrite crossings increases by a factor of $n$, to $$N_1 = n \phi /2\pi.$$
This was for one mitral cell. To account for all mitral cells, we note that the radial symmetry of the situation implies that the calculation for each mitral cell is the same. Therefore, we can compute the contribution from all mitral cells in an annular region around the granule cell by multiplying the contribution of one, $N_1,$ with the number of mitral cells contained in the annulus. For an annulus of radius $R$ and thickness $dR$, and a mitral cell density of $\rho$, the expected number of mitral cells is $\rho 2\pi R \; dR$.
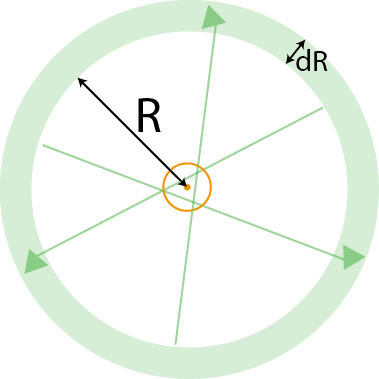
We integrate this contribution from the radius of the arbor to the maximum length at which a mitral cell could still contact the arbor, which is equal to the length of the lateral dendrites plus the radius of the arbor. That is,
\begin{align} N &= \int_{r}^{r + L} N_1\; \rho 2\pi R\;dR\\&= \int_{r}^{r + L} n {\phi \over 2 \pi} \rho 2\pi R\;dR\\&= 2 n \rho \int_{r}^{r + L} \arcsin\left( r \over R \right) R\;dR\\ &=n \rho \left[r R\sqrt{1 – {r^2 \over R^2}} + R^2 \arcsin\left(r \over R \right)\right]_{r}^{L+r}\end{align}
Assuming that the granule cell arbor $r$ is much smaller than the length of the lateral dendrites $L$, we have, using that $\arcsin(\varepsilon) \approx \varepsilon$,
$$ \boxed{N \approx n \rho (r L + L^2 (r/L)) = 2 n \rho r L.}$$
Some numbers
Let’s plug in some numbers from the mouse olfactory bulb. Mitral cells have about $n = 5$ lateral dendrites. As we mentioned above, the granule cell arbor is about $r = 100 \;\mu\text{m} = 0.1 \; \text{mm}$ in radius, and mitral cell lateral dendrites are $L = 1 \; \text{mm}$ long. There are about 20,000 mitral cells, distributed over a mitral cell layer of surface area $20\; \text{mm}^2$, so $\rho = 1000 \text{ mitral cells/mm}^2$. Then \begin{align}N &\approx 2 \times 5 {\text{lateral dendrites} \over \text{mitral cells}} \times {1000 \text{ mitral cells} \over \text{mm}^2 } \times {0.1 \text{ mm} } \times {1 \text { mm} }\\ &= 1000 \text{ lateral dendrites}.\end{align}
Simulation
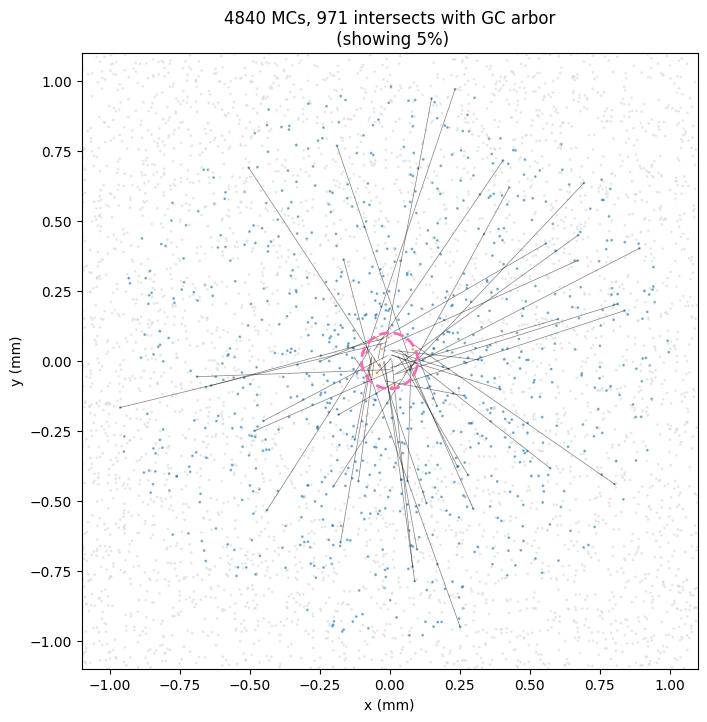
In this colab notebook I simulate the lateral dendrite intersections. Here’s an example output using the olfactory bulb numbers we used above.
We can also plot the effect of changing the parameters on the number of intersections, and compare that to the predictions.
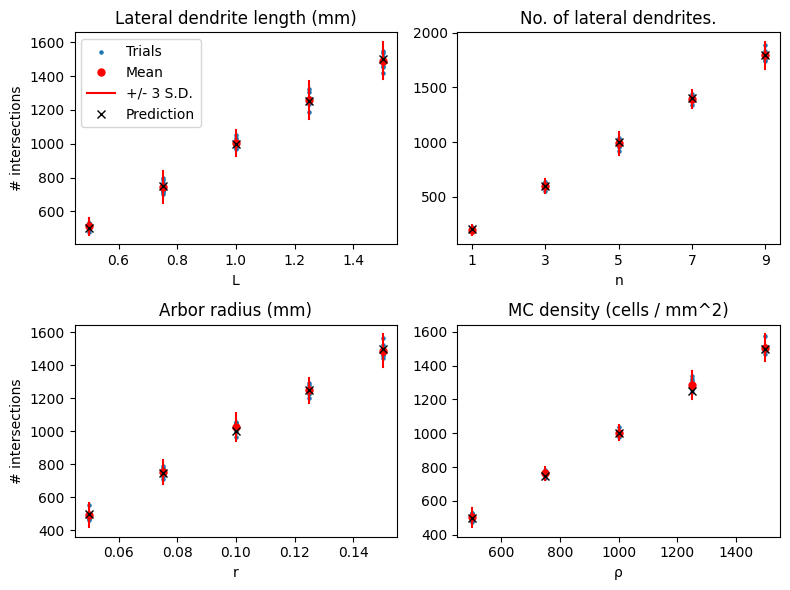
The results show good agreement with the predictions.
Core and periphery
An interesting aspect of the analysis is that it reveals the radial density of contributions to lateral dendrite intersections to be $$N_1 \rho \phi 2 \pi R = n \rho \arcsin(r/R) R \propto \arcsin(r/R) R.$$ This is plotted below.
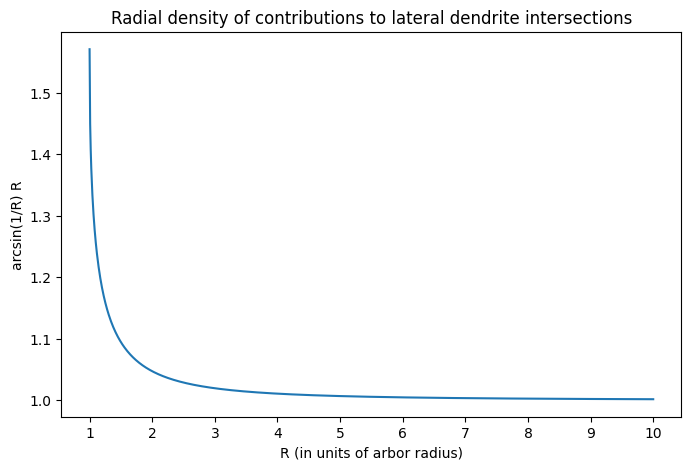
There are two interesting aspects about this plot. First is that the radial density increases dramatically as one approaches the arbor. This means that the mitral cells that are closer to the arbor will be much more likely to synapse onto it than those that are farther away. This suggests that there is a ‘core’ of mitral cells that drive the activation of a given granule cell.
Naively, this idea of a ‘core’ group of mitral cells suggests that the contribution from the remaining mitral cells, those in the ‘periphery,’ is limited. However, the second interesting aspect of the plot above indicates that this can in fact be false. Notice that the density of contributions does not decay to zero with distance from the arbor, but rather settles at a value of 1. This means that mitral cells in the periphery are equally likely to contact the arbor, regardless of distance. Since the number of mitral cells in an annulus around the arbor increases linearly with distance, this means that the contribution from the periphery can actually exceed that of the core. The balance between the two is determined by the length of mitral cell lateral dendrites, which determine the farthest a mitral cell can be from a granule cell and still make contact. Although the physical length of lateral dendrites is likely fixed, it may be possible to dynamically adjust their functional length through synaptic activity (see Xiong and Chen, 2002). This would then open up very intriguing possibilities for spatial computation.
Summary
We used a simple geometric model of the olfactory bulb to estimate how many lateral dendrites intersect a granule cell arbor, and found this number to be twice the product of the model parameters. The predictions were in good agreement with simulation results. We also discussed how the shape of the radial density of contributions to the lateral dendrite intersections suggests the existence of a ‘core’ and ‘periphery’ of mitral cells interacting with the granule cell, and how the balance between the core and the periphery can be modulated through dynamic gating of lateral dendrites.
Leave a Reply