In their 1993 paper Atick and Redlich consider the problem of learning receptive fields that optimize information transmission. They consider a linear transformation of a vector of retinal inputs $s$ to ganglion cell outputs of the same dimension $$y = Ks.$$ They aim to find a biologically plausible learning rule that will use the input statistics to find weights $K$ that optimize a particular loss function. Below we state the loss function and motivate it from the perspective of efficient coding. We will then work through their derivation of the learning rule.
Motivating the objective function
The loss function they minimize is $$E(K) = \tr(K R K^T) – \rho \log \det(K^T K).\label{obj}\tag{1}$$ Here the matrix $R = \langle s s^T\rangle$ contains the input correlations computed over time, and $\rho$ is a hyperparameter.
The first term: reducing signal energy
To motivate this objective from the perspective of efficient coding, we note that the first term is the expected energy of the outputs. This is because \begin{align} \tr(K R K^T) &= \tr(K \langle s s^T \rangle K^T)\\ &= \tr( \langle K s s^T K^T\rangle)\\ &= \tr(\langle y y^T \rangle)\\ &= \tr(\langle y^T y \rangle)\\&= \langle y^T y \rangle.\end{align}
If this was the only term in the objective then we could minimize it to its lowest possible value of zero by setting $K = 0$. The problem, of course, is that the resulting output, 0 for every input, also discards all the information present in the input signal.
The second term: preserving information
To minimize the output energy while preventing information loss, we use the second term in the objective. To see why this works, we apply the singular value decomposition to express $K$ as $U \Lambda V^T$. The energy of an output $y$ in response to an input $s$ can be expressed in terms of this decomposition as $$y^Ty = (U \Lambda V^T s)^T U \Lambda V s = s^T V \Lambda U^T U \Lambda V^T s = s^T V \Lambda^2 V^Ts.$$ The first thing to note is that the left singular vectors $U$ are absent from this expression. This reflects the fact that rotating the output $y$ does not change its energy.
Continuing, we can view $V^T s$ as rotating the input signal to produce $\tilde s$. In this rotated coordinate system, the energy of the transformed signal $y$ is just the sum of the energies of the rotated input signal along each of its dimensions, weighted by the squared singular values. That is, $$ y^T y = s^T V \Lambda^2 V^T s = \tilde s^T \Lambda^2 \tilde s = \sum_i \Lambda_i^2 \tilde s_i^2.$$ Since rotations preserve information, the only way that information could be lost is if one of the squared singular values, $\Lambda_i^2$, is zero. To prevent this we can penalize small singular values by their negative logarithm. The negative logarithm sends small values towards $\infty$ as they approach zero, penalizing them as we require. The second term of the objective is proportional to the sum of such penalties over all the singular values since
\begin{align} -\log \det(K^T K) &= -\log \det(V \Lambda^2 V^T)\\ &= -\log \det(\Lambda^2)\\ &= -\log \prod_i \Lambda_i^2\\ &= -2\sum_i \log \Lambda_i.\end{align} We can thus view the objective function as promoting energy efficiency while avoiding information loss,
$$ E(K) = \underbrace{\tr(K R K^T)}_{\text{energy minimization}} \quad \underbrace{- \rho \log \det(K^T K)}_{\text{information preservation}}, $$ with the parameter $\rho$ determining the balance between the two.
Convexity of the objective
To determine the optimal transformation that minimizes the output energy while preserving the information in the input signal, we minimize the loss $E(K)$. The first thing to note is that the loss is only a function of $K$ through $K^T K$, since by the rotational property of the trace, $$ E(K) = \tr(K R K^T) – \rho \log \det(K^T K) = \tr(R K^T K) – \rho \log \det(K^T K).$$ Therefore there is rotational redundancy in $K$ as $K \to U K$ produces the same $K^T K$ and hence the same loss. As mentioned above, this reflects the fact that rotating the outputs changes neither their energy nor their information content.
We can write the loss in terms of $G = K^T K$ as $$ E(G) = \tr(R G) – \rho \log \det(G).$$ Since the trace is convex and $\log \det$ concave in $G$, $E(G)$ is a convex function of $G$, being minimized over a convex domain, the set of positive definite matrices. Therefore, the loss function has a unique global minimum.
Optimality condition
To determine the value of $G$ that achieves this minimum, we compute the gradient $$ \nabla_G E = R^T – \rho G^{-1} = R – \rho G^{-1} = 0 \implies R G = \rho I,$$ where we’ve used that $\nabla_X \log \det(X) = X^{-1}$ and that the correlation matrix $R$ is symmetric. We see that the optimal $G$ inverts $R$, and is therefore unique.
The optimality condition $R G = I$ in terms of $K$ is (after dropping $\rho$), $$ R K^T K = I \implies K R K^T K = K.$$ Right-multiplying by $K^{-1}$ we arrive the optimality condition $$\boxed{K R K^T = I. \tag{2}\label{opt}}$$ Now $K R K^T = K \cov(s) K^T = \cov(Ks) = \cov(y)$. Therefore, we see that an optimal $K$ whitens the output – that is, it decorrelates the channels and equalizes their variances.
The rotational redundancy in $K$ is also present in the optimality condition, since $K \to U K$ still whitens the output because $$ U K R K ^T U^T = U U^T = I.$$
OPtimizing connectivity directly
Instead of working with $K^T K$, we can find optimal $K$’s by differentiating the loss in terms of $K$ itself. To compute the gradient, we compute the differential
\begin{align} dE &= \tr(dK R K^T) + \tr(K R dK^T) – \tr((K^T K)^{-1} d(K^T K)\\ &=\tr(R K^T dK) + \tr(dK^T K R) – \tr((K^T K)^{-1}(dK^T K + K^T dK)),\end{align} from which we read out the gradient as $$ \nabla_K E = 2 (KR – K (K^T K)^{-1}) = 2 (KR- K^{-T}),\label{Ek}\tag{3}$$ where in the last equality we’ve used that $K$ is square and invertible. Setting the gradient to zero we get $$ KR – K^{-T} = 0 \implies KR K^T = I,$$ the whitening condition in $\Eqn{opt}$ that we derived above.
Implementation in a feedforward circuit
At this point it’s useful to think about how all of this would occur in a neural circuit.
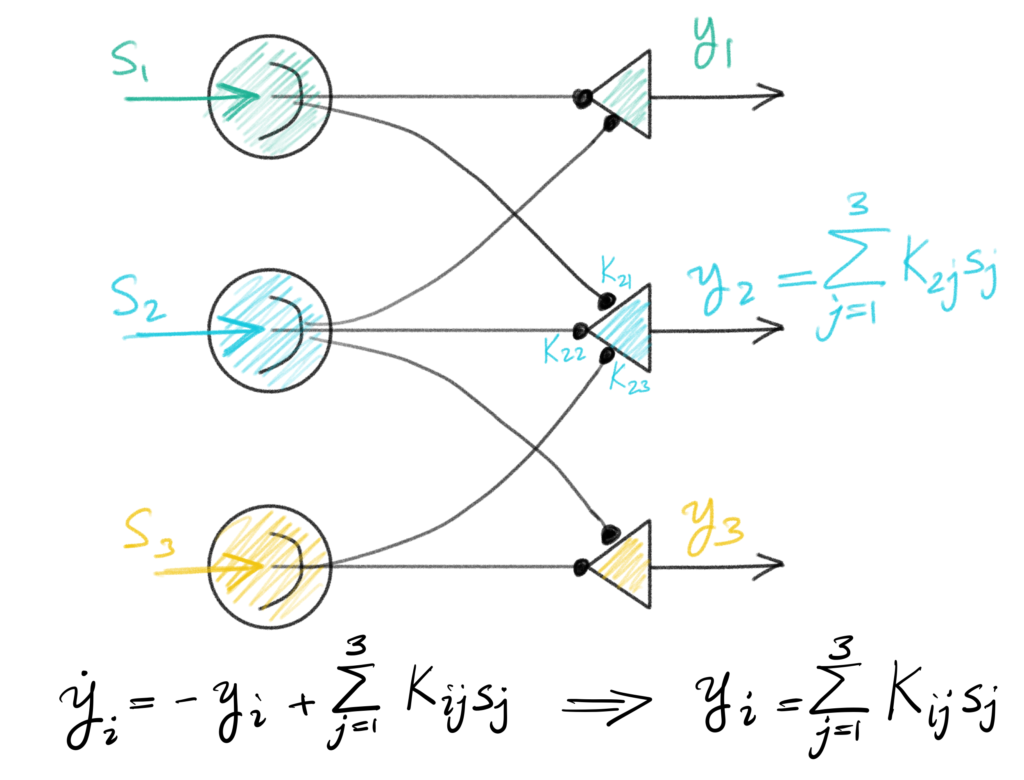
A simple circuit that would implement the action so far is the feedforward circuit shown above. Sensory inputs $s_1$ to $s_3$ excite the linear output units $y_1$ to $y_3$ through feedforward synaptic weights $K_{ij}$. The dynamics of the output units asymptotically converge to $y_i = \sum_{j} K_{ij} s_j,$ or in vector/matrix notation, $y = Ks$.
We’re interested in somehow learning the weights $K$ that optimize the objective in $\Eqn{obj}$. An obvious idea is to descend the gradient in $\Eqn{Ek}$ directly. This gives a learning rule like $$\delta K \propto -\nabla_K E = -KR + K^{-T}.\label{rule1}\tag{4}$$ Unfortunately this rule is not biologically plausible, because both terms on the righthand side make this rule non-local, since updating the strength of a synapse would require more information than is present at that synapse.
It’s easier to see this if we look at the rule element-wise and consider the update to synapse $K_{ij}$ neuron $i$ receives from input $j$. We would want such a rule to only involve quantities related to units $i$ and $j$, for example the synaptic strength itself $K_{ij}$, the output $y_i$ of neuron $i$, the input $s_j$ to neuron $j$, etc.
Instead, we have $$ \delta K_{ij} = -\sum_{n} K_{in} R_{nj} + (K^{-T})_{ij}.\label{rule1el}\tag{5}$$ The first term is already problematic because of the weighted sum over $K_{in}$ involves the synapses from all inputs to neuron $j$. But this might not be such a problem, since those quantities could still somehow be available at the soma of neuron $j$. Or, you might get lucky and your inputs arrive decorrelated. In that case $$R_{ij} \propto \delta_{ij} \implies \sum_{n} K_{in} R_{nj} \propto \sum_n K_{in} \delta_{nj} \propto K_{ij},$$ which is local. You could also try something more sophisticated and use the update $$ \delta K \propto -\nabla_K E R^{-1} = -K + K^{-T} R^{-1}.$$ This is still a descent direction (more on this below) so would still minimize the objective. It would also certainly solve the problem with the first term, since now $\delta K_{ij} = -K_{ij} + \dots.$ It also doesn’t require that $R$ by decorrelated, only that it be invertible, which we’re assuming it is.
The real problem is with the second term, which we’ve now exacerbated with our $R^{-1}$ term. Returning to the elementwise expression in $\Eqn{rule1el}$, we see that the update to the synapse $K_{ij}$ requires knowing the corresponding value of the transpose of the inverse of $K$. From Wikipedia, this value is $$(K^{-T})_{ij} = {C_{ji} \over \det(K)}, \quad C_{ji} = (-1)^{j+i} M_{ji},$$ where the minor $M_{ji}$ is the determinant of the submatrix left after removing the $j’\text{th}$ row and $i’\text{th}$ column.
If this sounds complicated, it is – determinants, minors etc. are global properties of a matrix. In synaptic terms, it means that to update $K_{ij}$, we need to know some complicated functions of all other synapses in the system, which is certainly not plausible.
An equivalent recurrent circuit
At this point we’re stuck – we have a well-motivated objective function in $\Eqn{obj}$ to evaluate feedforward connectivity $K$, but the learning rule we have in $\Eqn{rule1}$ is non-local, no matter how we have tried to finesse it. The way they get around this problem is by trying a different circuit.
To every feedforward circuit with (invertible) connectivity $K$, we can associate a recurrent circuit which produces the same asymptotic response to a given input. To see this, consider the circuit below:
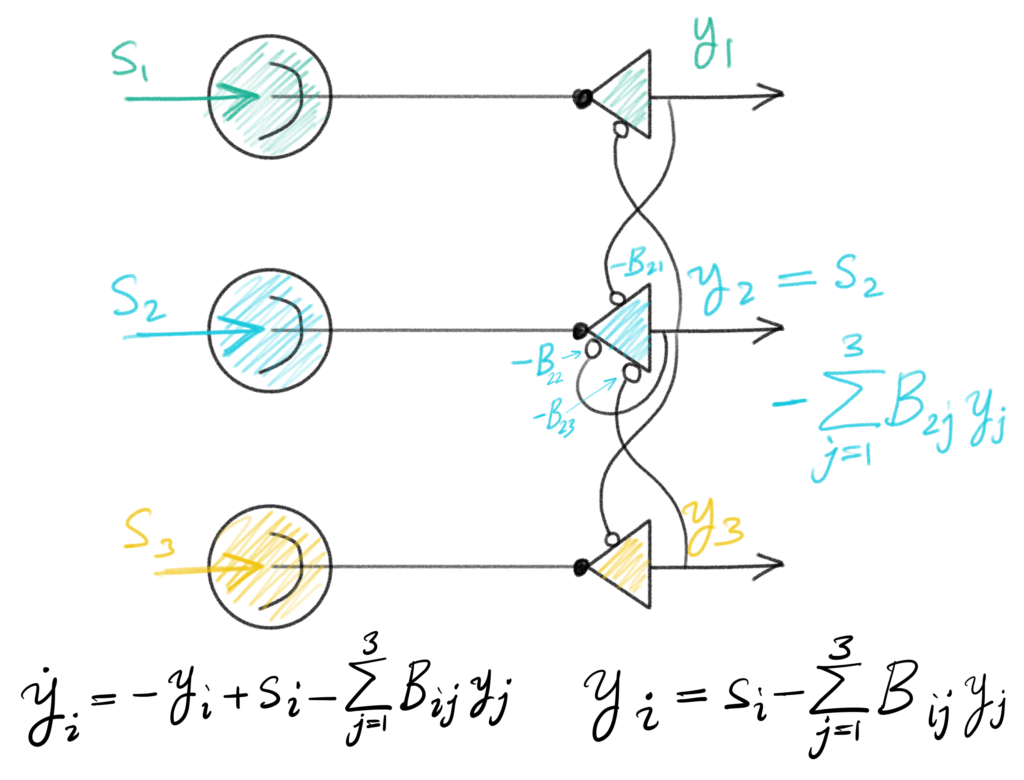
The all-to-all feedforward connections have been replaced with 1-to-1 connections from each input channel to a corresponding output unit. In contrast to the feedforward circuit, in which output units did not interact, in this recurrent circuit all output units interact, inhibiting each other with strength $B_{ij}$ (only some of the connections have been shown, for clarity). The circuit dynamics are $$ \dot y = -y + s – B y.$$
To see the connection to the feedforward circuit we determined the asymptotic value of the activity by setting the dynamics to zero. This gives $$y + B y = s \implies (I + B) y = s \implies y = (I + B)^{-1} s.$$ So we see that as far as asymptotic activity is concerned (and that’s all we’re concerned with here) a recurrent circuit with connectivity $B$ corresponds to a feedforward circuit with connectivity $K = (I + B)^{-1}$. If we call $W = (I + B)$, then we have that $K = W^{-1}$. In other words, a feedforward circuit with connectivity $K$ maps uniquely onto a recurrent circuit with connectivity $W = K^{-1}$.
Learning in the recurrent circuit
The problematic term in our feedforward learning rule was the inverse transpose, $K^{-T}$. We have just seen that a feedforward circuit $K$ maps onto a recurrent circuit with the inverse connectivity $W = K^{-1}$. So there might be hope that our learning rule $\Eqn{rule1}$, expressed in terms of $W$, might end up being local.
Instead, they use the update (defining $E_K \equiv \nabla_K E$) $$\delta K^T = -K^T E_K K^T.$$ This is still a descent direction of $E$ since \begin{align}\tr(\delta K^T E_K) &= \tr(-K^T E_K K^T E_K)\\ &=-\tr(E_K K^T E_K K^T )\\ &= -\tr((KRK^T – I)(KRK^T-I))\\ &= -\tr((KRK^T – I)(KRK^T – I)^T) \le 0,\end{align} where the inequality follows from $\tr(XX^T) \ge 0$ for all $X$.
Switching coordinates
Next they switch to $W = K^{-1}$ coordinates. These would be the weight that would convert the output to the input through $ W Y = S$. Another way to look at them would be in the lateral inhibition circuit $$ \dot Y = -Y + S – B Y \implies (I + B)^{-1} Y = S.$$ So $W – I$ would map on to the recurrent inhibitory weights $B$.
To determine the $W$ update, we use the fact that when $W = K^{-1}$, $\delta W = -K^{-1} \delta K K^{-1}$. We then substitute the transpose of our $\delta K^T$ update above to get $$\delta W = K^{-1}(K E_K^T K) K^{-1}= E_K^T = RK^T – K^{-1}.$$ Expressing $K$ in terms of $W$, we then get the dynamics $${dW \over dt} \propto \delta W = R W^{-T} – W.$$
It looks like we haven’t gained anything since we’ve again arrived at a nonlocal (through the inverse) learning rule. But unlike our nonlocal update of $K$, where the inverse term appeared alone, here the inverse of $W$ appears with $R$, which will allow us to express the updates as local (see below).
Convergence
We can show convergence of the updates using
\begin{align}{dWW^T \over dt} &= {dW \over dt} W^T + W {dW ^T \over dt}\\&= (RW^{-T} -W)W^T + W(W^{-1}R – W^T) \\ &= 2(R-WW^T),
\end{align} so $$WW^T(t) = R – e^{-2t} C,$$ where $C$ depends on the initial conditions. We see now that $WW^T$ converges exponentially to $R$. And this is the global minimum of the energy, since $$WW^T = R \implies W^{-1} R W^{-T} = K R K^{T} = I,$$ the whitening condition we found at the minimum.
A local implementation
It turns out that our nonlocal-looking update for $W$ can in fact be made local. This is because \begin{align} {d W \over dt} &= RW^{-T} – W \\ &= S S^T W^{-T} – W \\ &= S S^T K^T – W \\ &= S Y^T – W,\end{align} and we can convert this to an online update as
$$ {dW \over dt} = s(t)y(t)^T – W.$$
Choosing among solutions
We saw at the beginning that the loss $E(K)$ is actually only a function of $K^T K$, so does not determine $K$ uniquely. This was reflected again in the convergence condition requiring only that $WW^T = R$, and thus specifying $W$ only up to rotation. This means that although our weight dynamics will converge to a solution that will minimize our loss as desired, the particular solution found will depend on the initial conditions. Should we favour some solutions over others?
The authors argue on biological grounds for spatially localized receptive fields and therefore opt for the symmetric solution $W = W^T$. They explained why this solution would produce localized receptive fields, but I didn’t understand the explanation.
Summary
Atick and Redlich formulate the efficient coding problem as optimizing a loss that balances the coding energy against information preservation. By differentiating this with respect to connectivity they come up with a learning rule for the weights in a feedforward implementation. Unfortunately, the learning rule is non-local. However, by switching coordinates the the inverse of the feedforward connectivity, they managed to find a local learning rule for the resulting, recurrent, weights. The fact that this worked out in this case was a little miraculous, and it’s not clear why and under what conditions such a procedure would work in general.
$$\blacksquare$$
Leave a Reply