These are my notes from early January on Kondor et al.’s Multiresolution Matrix Factorization from 2014. This was a conference paper and the exposition was a bit terse in places, so below I try to fill in some of the details I thought were either missing or confusing.
Motivating MMF
We will be interested in factorizing $n \times n$ symmetric matrices $A$. MMF can be motivated through PCA, which gives the eigendecomposition $A = U^T D U,$ where $U$ is orthonormal and $D$ is diagonal. We can think of this as a compression if $U$ is known in advance. We can then encode $A$ (and other such matrices) by their projections onto $U$. For $A$, this is simply $$ U A U^T = D.$$ But we can imagine dealing with families of matrices and storing only their projections onto a fixed $U$. If $U$ is adapted to the family then these projections will be sparse, just like the diagonal matrix $D$ was (at most $n$ of the $n^2$ elements non-zero), and we will have achieved compression.
The problem with PCA is that the basis elements $U$ are non-local. That is, a given basis element will have lots of non-zero entries, implying that the corresponding projection requires information from many of the $n$ locations. This can make the projections hard to interpret.
MMF takes ideas from multiresolution analysis of functions on the real line and applies them to the discrete setting of $n$-dimensional vectors. It performs the decomposition of $A$ sequentially using a series of sparse orthonormal matrices. So our decomposition of $A$ will look like
$$ U_L U_{L-1} \dots U_{1} A U_1^T \dots U_{L-1}^T U_{L} = H,$$ where $H$ will also be diagonal except possibly on some central block. That is, we decompose the global rotation $U$ that a procedure like PCA might produce into a product of a sequence of local rotations $U_1, U_2, \dots U_L$.
The MMF Objective
To find the decomposition above we solve the optimization problem \begin{align} \min_{ \substack{[n]\supseteq S_1\dots S_L \\ U_1,\dots,U_L \in O \\ H \in H^n_{S_L}}} \|U_L \dots U_1 A U_1^T \dots U_L^T – H \|_F^2. \label{opt}\tag{1}\end{align}
Here the $[n]=S_0 \supseteq S_1 \dots S_{L-1} \supseteq S_L$ are nested subsets of the integers $1 \dots n$ that indicate the coordinates that can still be involved in rotations. All remaining coordinates are held fixed. $H_{S_L}^n$ is the set of matrices that are non-zero on the $S_L \times S_L$ block and also on the diagonal.
The first step is to eliminate the last constraint in the minimization ($H \in H_{S_L}^n$) by moving it to the norm itself. We do this by defining a ‘residual’ norm that only counts elements outside of the block and diagonal: \begin{align} \|X\|^2_\text{resi} = \sum_{\substack{(i,j) \not \in S_L \times S_L, \\ i \neq j }} X_{ij}^2. \label{resi} \tag{2}\end{align} So our problem becomes \begin{align} \min_{\substack{[n]\supseteq S_1\dots S_L \\ U_1,\dots,U_L \in O}} \|U_L \dots U_1 A U_1^T \dots U_L^T \|_\text{resi}^2. \label{resi2} \tag{3}\end{align} In other words, we’re looking for a sequence of rotations that diagonalize $A$, except possibly on the $S_L \times S_L$ block.
Multiresolution analysis of $\mathbb R^n$.
We now need to be careful about what the $U_i$ are. We first express $A$ as $$ A = \sum \la_i \xx_i \xx_i^T.$$ Each of the $\xx_i \in \RR^n = V_0$. The idea is now to split the base space $V_0$ into a direct sum of a ‘smooth’ subspace $V_1$ and a ‘detail’ subspace $W_1$: $$ V_0 = V_1 \oplus W_1.$$
Let a basis for $V_1$ be the rows of $\Phi_1$ and a basis for $W_1$ the rows of $\Psi_1$. We can express these basis elements in terms of the basis $\Phi_0$ for $V_0$ using the matrix $U_1$: $$ \begin{bmatrix} \Phi_1 \\ \Psi_1 \end{bmatrix} = U_1 \Phi_0.\label{basis0}\tag{4}$$ Since $\dim(\Phi_1) = \dim(V_1)$ and $\dim(\Psi_1) = \dim(W_1)$ and $\dim(V_1) + \dim(W_1) = \dim(V_0)$, $U_1$ has dimensions $\dim(V_0) \times \dim(V_0) = n \times n$. We additionally require that $U_1$ is orthonormal, i.e. $U_1^T U_1 = I$.
We can now express $A$ in the $\Phi_1 \cup \Psi_1$ basis by first using $\Eqn{basis0}$ to express $\Phi_0$ in this basis: \begin{align} U_1^T \begin{bmatrix} \Phi_1 \\ \Psi_1 \end{bmatrix} = \Phi_0 \implies \Phi_0^T = \begin{bmatrix} \Phi_1^T | \Psi_1^T \end{bmatrix} U_1.\end{align} Then $$ \xx_i = \Phi_0^T \xx_i = \begin{bmatrix} \Phi_1^T | \Psi_1^T \end{bmatrix} U_1 \xx_i.$$ The first $\dim(V_1)$ rows of $U_1$, whose projections on $\xx_i$ are projected out with $\Phi_1^T,$ are then the scaling functions, and the remaining rows are the wavelets.
So the coefficients expressed in the new basis are $U_1 \xx_i$. Therefore, $$ A_1 = \sum \la_i U_1 \xx_i (U_1 \xx_i)^T = U_1 \left( \sum \la_i \xx_i \xx_i^T \right) U_1^T = U_1 A U_1^T.$$
To continue with the multiresolution analysis, we split $V_1 = V_2 \oplus W_2$ and define $U_2$ as the matrix that expresses $\Phi_2$ and $\Psi_2$ in terms of $\Phi_1$: $$ \begin{bmatrix} \Phi_2 \\ \Psi_2 \end{bmatrix} = U_2 \Phi_1.$$ The dimensions of $U_2$ are $\dim(V_1) \times \dim(V_1)$, and as before we also require that $U_2$ is orthogonal, i.e. $U_2^T U_2 = I$. To make it compatible with $A_1$, we extend it with the identity matrix, so that it leaves the $W_1$ subspace unchanged: $$ U_2 \leftarrow U_2 \oplus I_{\dim(W_1)}.$$ Then, following the same reasoning as before, we can express $A$ in the $\Phi_2 \cup \Psi_2 \cup \Psi_1$ basis as $$ A_2 = U_2 A_1 U_2^T = U_2 U_1 A U_1^T U_2^T.$$ The first $\dim(V_2)$ rows of $U_2 U_1$ are the scaling functions, the next $\dim(W_2)$ rows are the wavelets from $W_2$, and the remaining rows are the wavelets from $W_1.$ Continuing in this way for $L$ steps, we get the optimization problem $\Eqn{opt}.$
Recursive decomposition
To solve our optimization problem $\Eqn{opt}$ we work with its residual-norm formulation $\Eqn{resi2}$ and expand it recursively. First, let’s apply a recursive decomposition to the ordinary Frobenius norm. Since $S_0 = [n]$, we start with $$ \|H\|^2 = \|H_{S_0, S_0}\|^2$$. This is the sum of squares of all the elements of $H$. The next set of indices, $S_1$ are a proper subset of $S_0$, so we can decompose our sum as
$$ \|H_{S_0, S_0}\|^2 = \|H_{S_1, S_1}\|^2 + \|H_{S_1, S_0/S_1}\|^2 + \|H_{S_0/S_1,S_1}\|^2 + \|H_{S_0/S_1,S_0/S_1}\|^2.$$ Letting $J_i = S_{i-1}/S_i$ indicate the indices $S_{i-1}$ contains that $S_i$ doesn’t, we can write the last expression as $$ \|H_{S_0, S_0}\|^2 = \|H_{S_1, S_1}\|^2 + \|H_{S_1, J_1}\|^2 + \|H_{J_1,S_1}\|^2 + \|H_{J_1,J_1}\|^2.$$ We can pack all the terms that index $J_1$ into $\mathcal E_1$ and get $$ \|H_{S_0, S_0}\|^2 = \|H_{S_1, S_1}\|^2 + \mathcal{E}_1.$$
We can similarily decompose $\|H_{S_1,S_1}\|^2$, to get \begin{align}\|H_{S_0, S_0}\|^2 &= (\|H_{S_2, S_2}\|^2 + \|H_{S_2, J_2}\|^2 + \|H_{J_2,S_2}\|^2 + \|H_{J_2,J_2}\|^2) + \mathcal{E}_1\\ &= \|H_{S_2, S_2}\|^2 + \mathcal{E}_2 + \mathcal{E}_1.\end{align} Continuing in this way, we get $$\|H\|^2 = \|H_{S_0, S_0}\|^2 = \|H_{S_L, S_L}\|^2 + \sum_{\ell=1}^L \mathcal{E}_\ell.$$
Therefore, if we redefine $\mathcal{E}_i$ to not include the diagonal terms, $$\mathcal{E}_\ell = 2 \|H_{J_\ell, S_{\ell}}\|_F^2 + \|H_{\substack{J_\ell, J_\ell\\ \text{off diag}}}\|^2, \label{Eell} \tag{5}$$ we arrive at $$\|U_L \dots U_1 A U_1^T \dots U_L^T \|_\text{resi}^2 = \|H\|_\text{resi}^2 = \sum_{\ell=1}^L \mathcal{E}_\ell.$$
We’d now like to express $\Eqn{Eell}$ succinctly in terms of $A$ and the $U$’s. To do so, notice that $U_{\ell+1}$ is the identity on its lower $S_0/S_{\ell}$ block. So, with some abuse of notation, \begin{align} A_{\ell+1} = U_{\ell+1} A_{\ell} U_{\ell+1}^T &= \begin{bmatrix} U_{\ell+1} & 0 \\ 0 & I_{S_0/S_{\ell}} \end{bmatrix} \begin{bmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{bmatrix} \begin{bmatrix} U_{\ell+1}^T & 0 \\ 0 & I_{S_0/S_{\ell}} \end{bmatrix}\\ &= \begin{bmatrix} U_{\ell+1} A_{11} & U_{\ell+1} A_{12} \\ A_{21} & A_{22} \end{bmatrix} \begin{bmatrix} U_{\ell+1}^T & 0 \\ 0 & I_{S_0/S_{\ell}} \end{bmatrix}\\ &= \begin{bmatrix} U_{\ell+1} A_{11} U_{\ell+1}^T & U_{\ell+1} A_{12} \\ A_{21} U_{\ell+1}^T & A_{22} \end{bmatrix}. \end{align} Then $$ \|[A_\ell]_{J_\ell, S_\ell}\|_F^2 = \|[A_\ell]_{S_\ell, J_\ell}\|_F^2 = \|[A_{12}]_{:,J_\ell}\|_F^2,$$ where we’ve abused notation on the final set of indices and used the absolute indices $J_\ell$ instead of those relative to $A_{12}$. Next, $$ \|[A_{\ell+1}]_{J_\ell, S_\ell}\|_F^2 = \|[A_{\ell+1}]_{S_\ell, J_\ell}\|_F^2 = \|[U_{\ell+1} A_{12}]_{:,J_\ell}\|_F^2 = \|[A_{12}]_{:,J_\ell}\|_F^2 = \|[A_\ell]_{S_\ell, J_\ell}\|_F^2,$$ where the third equality is because Frobenius norm is invariant to rotation. But this will then hold for all $\ell + k$, because $U_{\ell+k}$ is a rotation on a subspace of that on which $U_{\ell+1}$ acts. Therefore $$ \|H_{J_\ell, S_\ell}\|_F^2 = \|[A_L]_{J_\ell, S_\ell}\|_F^2 = \|[A_\ell]_{J_\ell, S_\ell}\|_F^2.$$
The only term that remains in $\Eqn{Eell}$ is $\|H_{J_\ell, J_\ell}\|_F^2$ (without the diagonal terms) – but these will be part of $A_{22}$, which is left unchanged in $A_{\ell+1}$. Therefore, we can write $$ \mathcal{E}_\ell = 2 \|[A_\ell]_{J_\ell, S_\ell}\|_F^2 + \|[A_\ell]_{\substack{J_\ell, J_\ell \\ \text{off diag}}}\|_F^2.$$
Notice that $S_\ell$ is potentially a large set, while the rotations might be operating on small subsets of this. The rotation $U_\ell$ can operate on any of $S_{\ell-1}$. Let’s suppose that:
- It operates on a subset $I$, so that $U_\ell = I_{n-k} \oplus_I O$, where $k=|I|$. Then $S_{\ell-1} = I \cup \overline{S_{\ell-1}}$;
- That $i_k \in I$, so $S_{\ell} = (I/\{i_k\}) \cup \overline{S_{\ell}}$, and $\overline{S_{\ell}} = \overline{S_{\ell-1}}$.
In that case, $J_\ell = S_{\ell-1} / S_\ell = \{i_k\}$, and we can write the above as \begin{align*} \mathcal{E}_\ell &= 2 \|[A_\ell]_{i_k, S_\ell}\|_F^2\\ &= 2 \|[A_\ell]_{i_k, I/i_k}\|_F^2 + 2 \|[A_\ell]_{i_k, \overline{S_\ell}}\|_F^2\\ &= 2\sum_{i=1}^{k-1}[O A^{\ell-1}_{I,I} O^T]^2_{k,i} + 2[OA^{\ell-1}_{I,\overline{S_\ell}} (A^{\ell-1}_{I,\overline{S_\ell}})^T O^T]_{k,k} \end{align*} We now have to minimize this over $O \in SO(k)$.
Remark: It seems that the problem is a bit easier than this. We can write \begin{align*} \mathcal{E}_\ell &= -2 [O A_{I,I}^{\ell-1} O^T]^2_{k,k} + 2\sum_{i=1}^{k}[O A^{\ell-1}_{I,I} O^T]^2_{k,i} + 2[OA^{\ell-1}_{I,\overline{S_\ell}} (A^{\ell-1}_{I,\overline{S_\ell}})^T O^T]_{k,k}\\ &= -2 [O A_{I,I}^{\ell-1} O^T]^2_{k,k} + 2 [O A^{\ell-1}_{I,I} A^{\ell-1,T}_{I,I} O^T]_{k,k} + 2[OA^{\ell-1}_{I,\overline{S_\ell}} (A^{\ell-1}_{I,\overline{S_\ell}})^T O^T]_{k,k} \end{align*} But this only depends on $k$’th row of $O$, $o_k$: \begin{align} \mathcal{E}_\ell &= -2 [o_k A_{I,I}^{\ell-1} o_k^T]^2 + 2 o_k A^{\ell-1}_{I,I} A^{\ell-1,T}_{I,I} o_k^T + 2 o_k A^{\ell-1}_{I,\overline{S_\ell}} (A^{\ell-1}_{I,\overline{S_\ell}})^T o_k^T\\ &= -2 [o_k A_{I,I}^{\ell-1} o_k^T]^2 + 2 o_k \left[A^{\ell-1}_{I,I} A^{\ell-1,T}_{I,I} + A^{\ell-1}_{I,\overline{S_\ell}} (A^{\ell-1}_{I,\overline{S_\ell}})^T\right] o_k^T\\ &= -2 [o_k F o_k^T]^2 + 2 o_k G o_k^T. \end{align} We now want to minimize this subject to $\|o_k\| = 1$. Renaming $o_k$ to $x^T$, we get $$ \min_{x^T x =1} -(x^T F x)^2 + x^T Gx.$$ The Lagrangian is $$ L(x, \la) = -(x^T F x)^2 + x^T G x + \la (1 – x^T x) .$$ The gradient is $$ L_x \propto -2 (x^T F x) F x + G x – \la x .$$ So at the optimum, \begin{align*} x &= \la^{-1} (G x – 2 (x^T F x) F x)\\ \la &= x^T G x – 2 (x^T F x)^2. \end{align*}
This is an eigenvalue equation for $(G – 2(x^T F x) F)$, but since the scaling of $F$ depends on $F$, we can’t solve it straightforwardly that way. Instead, we can try solving this system using it as an update equation. This is how I do it in the function solve in my implementation of MMF.
Code
I have written a Python implementation of the algorithm below in this repo. The notebook contained there applies MMF to a matrix of odour-odour correlations, as shown below.
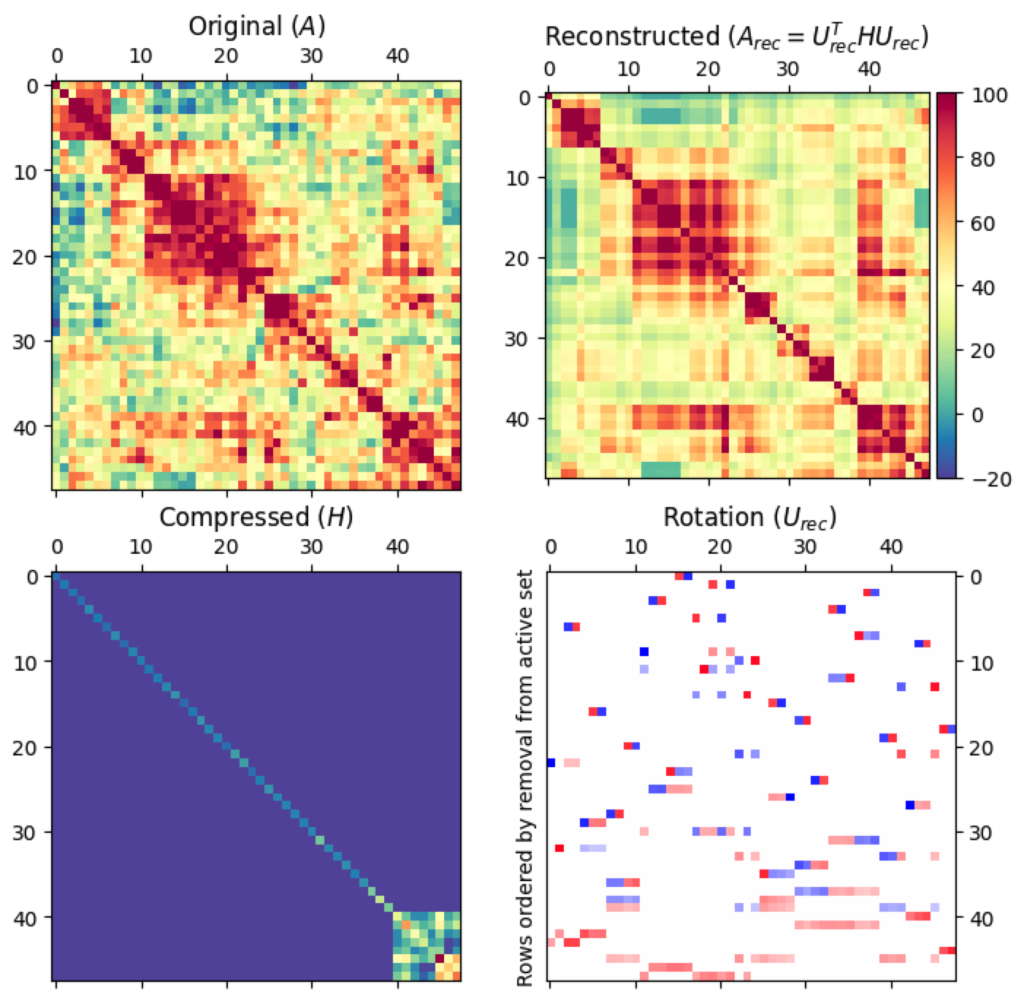
Notice how, in the bottom right panel, early features are ‘high-frequency’, consisting of large rotations of small numbers of matrices. Later features to be smoother, and integrate over more indices. Perhaps this is how the “multiresolution” aspect manifests, just like how when analyzing functions on the real line, the subspaces later in the analysis capture smoother features.
$$\begin{flalign*} && \phantom{a} & \hfill \square \end{flalign*}$$
Leave a Reply