We are trying to understand the connectivity solutions $Z$ found when minimizing the objective $$ {1 \over 2 n^2 } \|X^T Z^T Z X – C\|_F^2 + {\la \over 2 m^2}\|Z – I\|_F^2.$$
Recap
We found in the previous post that solutions satisfy
$$ {1 \over \la’} \left(S^2 \wt Z_{UU}^2 S^2 – S \wt C_{VV} S \right) + I = \wt Z_{UU}^{-1},\tag{1}\label{eqn:main}$$ where $\wt Z_{UU} = U^T Z U$,$\wt C_{VV} = V^T C V$, and $\la’ = {\la n^2 / 2 m^2}.$
Then,
- We noticed that the left-hand side looks like an arrowhead matrix and to determine $\wt Z_{UU}$ we had to invert.
- Arrowhead matrices are determined by their first column or first row, $h$, so $\wt Z_{UU}$ depended on this quantity.
- We found that if we used the observed value of $h$, then the approximation of $\wt Z_{UU}$ was good. This suggests the arrowhead approximation is OK, if we get $h$ right.
- In practice we need to determine $h$ from the other quantities in the problem. The relationship of the vector $h$ to the other quantities in the problem is complex.
- We tried to approximate $h$ by its first element, that is $h \approx h_1 e_1$, and the solving for $h_1$ in terms of the other parameters.
- The resulting estimate for $h_1$ was about 30 times less than its correct value!
- I guessed that this was due to how $\wt Z_{UU}$ is sandwiched between two $S^2$ terms, so any errors, e.g. due to poor approximations, will get amplified and affect other parameter estimates.
I then worked on trying to improve the approximation of $h$ – in particular by including a term to account, not for the values of all the other terms in $h$, but for their squared norm, which seemed to be the important quantity. I didn’t get very far with that.
A solution?
The solution I found today sidesteps this issue. Due to optimization tolerances, the solution to $\Eqn{eqn:main}$ returned by the minimization procedure isn’t exact. We can look for the exact solution by running that equation as a damped iteration,
$$ Z_{t+1}^{-1} = \alpha Z^{-1}_t + (1- \alpha)\left[{1 \over \la’} \left(S^2 Z_t^2 S^2 – S \wt C_{VV} S \right) + I\right].$$ Below I’ve plotted the before and after:
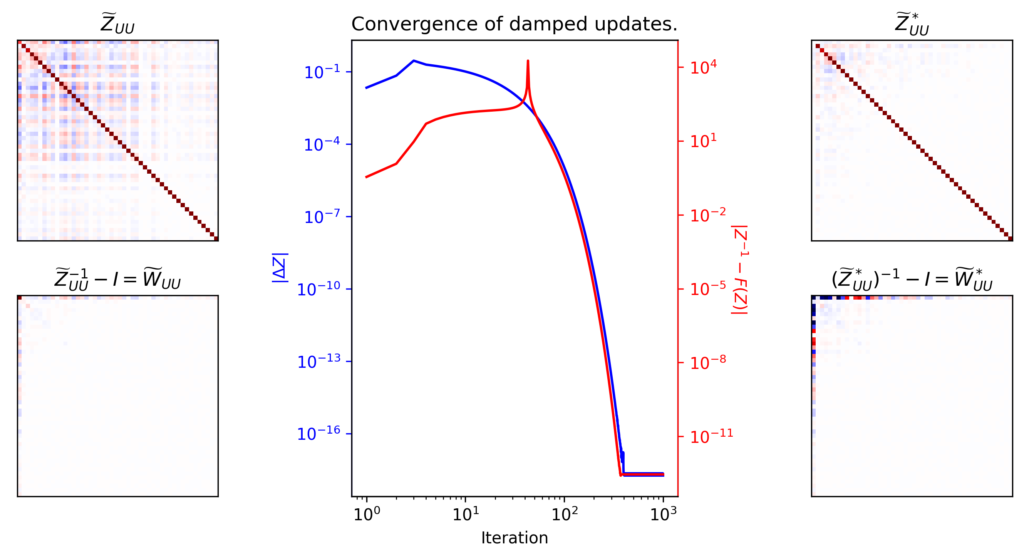
The left two panels show $\wt Z_{UU}$ returned by the optimization, and the corresponding recurrent weights $\wt W_{UU}$. I uses $\wt Z_{UU}$ to start the iteration. The plot in the middle shows that, after some transient divergence, the iterates get closer together (blue) and converge to a solution (red). The solution, shown on the right, satisfies $\Eqn{eqn:main}$ at numerical precision. It’s clear that the initial and terminal solutions are quite different. For example $\wt Z_{UU}$ seems to have a lot of off-diagonal elements, whereas these are suppressed in $\wt Z_{UU}^*$. The latter also seems to have its first element almost at zero. This seems well located to cancel the effect of the sandwiching $S^2$ terms.
What makes $\Eqn{eqn:main}$ hard to solve is that $Z$ shows up in two places: as a $Z^{-1}$ on the righthand side, and as $Z^2$ on the left. The problems we were seeing last time were due (I believe) to errors in our estimate being amplified through the term on the left. Ideally, we’d like to be able to ignore one or the other term to have a hope of solving this equation. However, when we use the optimization solution, the term on the right is a little bigger than the term on the left. So we have to consider both.
Interestingly, using the exact solution, the contribution of the term containing $Z^2$ is much smaller than that of the term on the right, by about a factor of 60 when measured in matrix norm.
Is this just a happy coincidence?
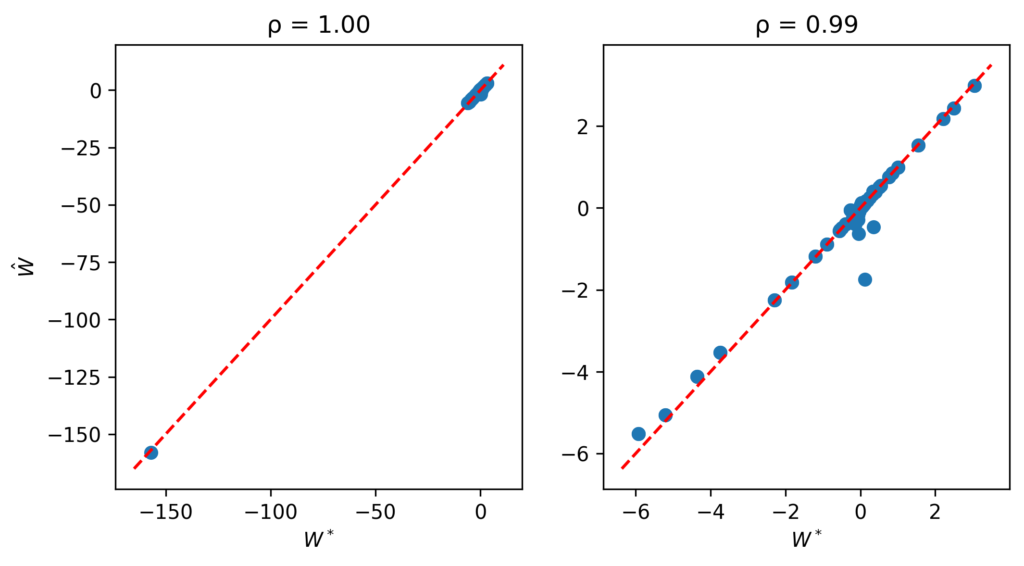
If we drop the $Z^2$ term, we get $$ \wt Z_{UU}^{-1} – I = \wt W_{UU} \approx -{S \wt C_{VV} S \over \la’}.$$ This is in fact in good agreement with the true value:
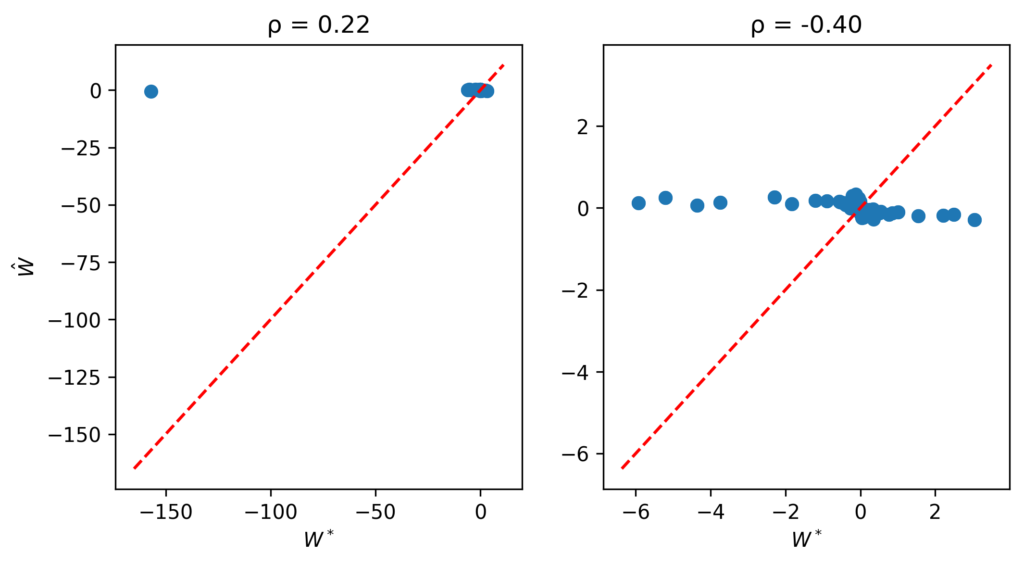
This is definitely not the case if we use the solution returned by the optimization:
Leave a Reply